"Other Nonlinear Functions" consists, in our case, of general polynomials and rational functions. There are numerous other nonlinear functions, including exponential and logarithmic (which we will see in another section), some of which are referred to as "transcendental functions" because they can't be evaluated using standard algebraic calculations (addition, multiplication, or powers). Here is a spreadsheet with some graphs of polynomial and rational functions that can be modified to display the function of your choice.
Polynomials
A
polynomial function is just an extended, more general form of the quadratic
function. It might involve more powers of x than just x
or x2, and as a result may involve more complex ups
and downs. Detailed analysis is obviously more complicated. In fact, for
our purposes we are satisfied with rather broad observations.
We tend to describe a polynomial with a function in the form, y = f(x) = a0 + a1x + a2x2 + ... + anxn, where a0...an are coefficients of the corresponding powers of x. n is the highest power of x in the function and is referred to as the "degree" of the polynomial.
The degree (4 in the example here) is an indication of the complexity, allowing up to n x-intercepts and n-1 turning points in the polynomial.
The "leading term" is the one containing the highest power of x and governs the dominant behavior of the polynomial. If n is odd, the function will be "odd" (starting in one quadrant and ending in the one diagonally opposite). If n is even, the function will be "even" (ending in the quadrant adjacent to the one it starts in). The coefficient, an, will determine the direction of the function. If it is negative, the function will eventually drop off negative on the right. If the coefficient is positive, the function will eventually end up increasing on the right.
The constant coefficient, a0, describes the y-intercept, just like in linear or quadratic functions.
Occasionally (although not always), the polynomial can be written in factored form, y = f(x) = an(x-x1)(x-x2)...(x-xn). For as many factors as can be found, up to n of them, x1...xn, are the x-intercepts of the polynomial. There is no algebraic formula (like the quadratic) for finding these values when n is greater than 4. However, there are numerical techniques that will calculate any real values, such as this java applet.
Rational Functions
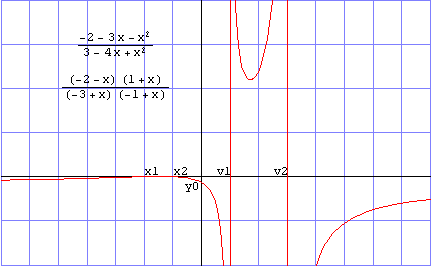Rational
functions are functions that can be written as, y = f(x) = n(x)/d(x),
where n(x) and d(x) are polynomials. Their most notable
feature is the somewhat strange behavior at the values of x where
d(x) = 0. Unlike other functions discussed so far where any value
of x produces a real value of y, y in this
case is undefined when d(x) = 0, leading us to state that those
points are NOT part of the domain of the function. In fact, as long as
n(x) isn't 0 as well, we refer to these as vertical asymptotes,
because the function tends to "blow up" (get very large, either
negative or positive) as x approaches these values.
Rational functions have x and y-intercepts that can be found in a similar way to polynomials. Set x = 0 to find y-intercepts and set n(x) = 0 to find x-intercepts.
With polynomials we discussed the dominant behavior, whether even or odd, positive or negative, depending upon the leading term. Something comparable happens with rational functions, but what we look at instead is the ratio of the leading term from n(x) divided by the leading term of d(x). Something interesting happens when the powers of x cancel out (n(x) and d(x) have the same degree) - the dominant behaviour is essentially constant, which we refer to as the "horizontal asymptote." This means that at large values of x (negative or positive) the function levels out at the value indicated by the ratio of leading coefficients. If the denominator has a higher degree than the numerator, the function will just level out at zero.
Contact Leo Wibberly at ldwibber@vcu.edu or (804) 740-4650 to make appointments