The most natural and widely applicable nonlinear function is probably the exponential function. It describes any growth or decay of a quantity that is proportional to the existing quantity. The typical examples of this are compound interest, where the yield is some percentage of the current balance, or population growth, where the number of new births tends to get larger as the population gets larger. In general this function looks like y = f(x) = a b^x, where a is the intial value of the function and the base b (greater than 0) determines how fast it grows (if b>1) or decays (if b<1) from that point.

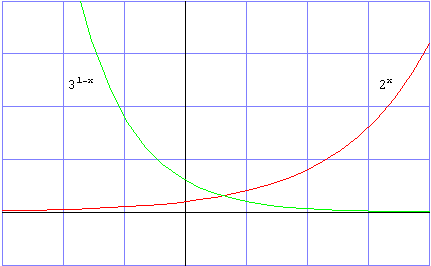
The two functions here represent growth (y = 2^x) and decay (y = 3^1-x = 3 (1/3)^x) with different y-intercepts (1 and 3 respectively). It can also be seen that the decay (1/3) is faster than the growth (2) - if the decay were 1/2 insteand of 1/3 you would see functions that are mirror images of each other.

To manipulate exponential functions it is handy to be familiar with the various algebraic properties of expressions involving powers. In particular there are the identities:

• b^-x = (1/b)^x
• (b^x)^y = b^xy
• b^xb^y = b^x+y
• (a b)^x = a^x b^x

Rather than representing different exponential functions with a different base, it is common in scientific circles to always use the same base and raise it to a power r that indicates the growth (r>0) or decay (r<0) rate. The actual base used is an irrational number e = 2.71828..., that is defined as (1+1/n)ⁿ when n gets very large and shows up in so many areas of mathematics that it is referred to as the "natural base." For example, with the two functions displayed above, it can be shown that 2.71828^0.69135 = 2 and 2.71828^-1.09861 = 1/3. This means that the growing exponential can be rewritten as y = a e^rx = e^0.69135x by replacing the 2 and the decaying function can be expressed as y = 3e^-1.09861x by replacing the 1/3. The exponential trendlines calculated in Excel always use the natural base form ae^rx, while the regression analysis performed on most calculators (Texas Instruments at least) typically find an exponential fit of the form ab^x, however they are interchangeable.

The primary purpose of this section is not so much to write the proper equations or graph them as it is to solve equations involving exponential relationships. After some amount of algebraic manipulation involving the identities listed above, most equations with an exponential in them and a single unknown quantity can be simplified to look like c = b^d, where either c, b, or d can be algebraic expressions involving the unknown, call it x. This leaves three possible scenarios.

1. x is part of the expression c, in other words c(x) = b^d. Then b^d is an easily calculated number, just solve for x.
2. x is part of b, so c = b(x)^d. Just use the principle that c^1/d = (b(x)^d)^1/d = b(x), then solve for x.
3. And the real challenge, c = b^d(x). This requires us to know how to express c as a power of b. c = b^y, so we can subsitute it in the equation and get b^y= b^d(x) or y = d(x). If we knew y we could solve for x. The question becomes, how do we calculate y, the power necessary to raise b to in order to get c?

It turns out there is a name for this process. It is called the "inverse exponential" (instead of finding the result of a power we find the power necessary for a given result, sort of like Goalseek in Excel) or, more precisely, the "logarithm base b of c." Thus any equation that looks like c = b^y can be rewritten as y = log_bc. Now there is no nice way to calculate this value by hand so you need a computer or calculator to do it for you. Even more awkward, most calculators will only calculate logarithms in two bases, b=10 (referred to as just log) and b=e (referred to as ln). So if your equation has a 10 raised to some power, or an e raised to some power, you are in luck. Fortunately there is a way around this limitation, but it requires some knowledge of properties of logarithms (similar to the exponential properties listed above).

• log_b(1/c) = - log_bc
• log_b(a c) = log_ba + log_bc
• log_b(c ⁿ) = n log_bc

So, back to the original problem, solving c = b^d(x). Take the logarithm base 10 of both the left and right side to maintain equality. This gives us log c = log (b^d(x)) = d(x) log b. If you divide both sides by the quantity multiplying d(x), you will get d(x) = log(c)/log(b), which can easily be solved for x. If b=10, this turns out to be d(x) = log c. If b=e, the equation becomes d(x) = ln c.

Now you can solve anything! Well there are a few functions involving exponentials, like the "limited growth" or the "logistic curve" that look a bit weird, but a little algebraic manipulation will work wonders on them.

Contact Leo Wibberly at ldwibber@vcu.edu or (804) 740-4650 to make appointments