General strategy

Many are tempted to take the tools described in other sections and hammer away at T4, hoping by sheer brute force to obtain new single insertion/deletions and then doubles, and finally three insertions or deletions. You are not a brute! If you find yourself repeating the same operation over and over, consider pausing and using that time to think more deeply about the problem, perhaps consulting with resources or people to enable you to use your time more effectively through simple selections and straight-forward screens.

Although you wouldn't know it from the original Crick et al (1961) article [3], there are simple tricks that enable you to whizz through the process of constructing the desired mutations. The ultimate trick leading to a triple mutant relies on a great genetic map, similar to Figure 2 of Crick et al (1961). To get such a map is a lot of work, but you are not alone! I've provided tools to enable you to share the burden with your colleagues to arrive at a community-derived genetic map.

How to make new single insertion/deletions

No clever tricks are necessary for this task -- simply select for a mutation that suppresses the effect of one of the insertion/deletion R- strains provided to you (see the VARIABLE menu after loading the simulation).Suppressor mutations are rare (see How many phages to use in experiments), but that's hardly a problem when you have a powerful selection -- the abiity of a R+ phage with a suppressor mutation to grow on E. coli K12. Mutagenizing a sufficient number of phages carrying FC0 or one of the other insertion/deletion mutations and plating on K12 should net you as many suppressor mutations as you can handle...

... so long as you separate the new suppressor mutation from the old suppressed mutation on the same phage. This is done thrugh an easy screen -- co-infecting the phenotypically wild-type strain containing both mutations with true wild-type phage T4, allowing recombination to produce R- progeny with only one mutation and a large-plaque phentype on E. coli B. This should be a very easy screen. All of the suppressors of FC0 (+) should be of opposite sign, according to Crick et al (1961). You can check this by determining if any of the supposedly (-) mutations can suppress another (-) mutation.

Mapping mutations

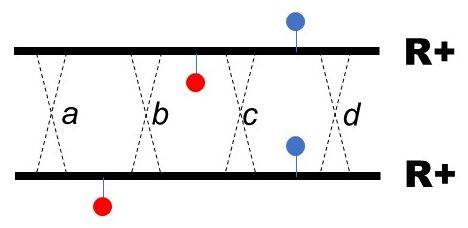
Looking ahead to the later steps, any separated R- single mutant should be accurately mapped relative to an agreed upon location. I've chosen FC0 as our anchor, so the map position of a mutation will reported as its distance from FC0, either positive (to the right) or negative (to the left). The map distance between two mutations is proportional to the frequency of recombination between the two. The strategy therefore is to cross every single ins/del mutantion with FC0 to measure the frequency of recombination between the two mutations. See How to do the simulation for tips on how to map.

How to make double (-)(-) or (+)(+) mutations

At first glance, the probem seems virtually un-doable. If individual (-) mutations are R- and rare (-)(-) recombinants also figure to be R-, then how do you find them in the crowd? The trick is to do a cross where the recombinant progeny have a different phenotype than their parents. Here's how. Look at Figure 1, which shows two R+ strains resulting from the suppression of one ins/del mutation by another. Both are R+. If you coinfect the two strains, some of the rare recombination events (a through d) will lead to easily screened R- recombinants and some won't. Go through each one and decide what you'll get. Not all the R- recombinants will be the red-red-blue mutation you want, but a large fraction will be, and it won't be difficult to tell which is which, by crossing the R- progeny with a single R- strain. 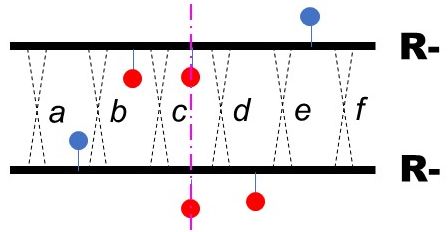Of course, this procedure does not get you a pure red-red mutant -- it remains contaminated with a mutation of the opposite sign, but keeping our eye on the big prize, that's OK.

Figure 1: suppression of blue (-) or (+) mutation with a red (+) or (-).

How to make triple (-)(-)(-) or (+)(+)(+) mutations

These are very difficult to obtain, unless you take the provisional view that triple mutants might be R+. Then it's not too hard. Figure 2 shows two double mutants of the type produced as described in the previous section. If you follow each of the six possible recombinatino events, you'll find two that produce a clean triple mutant. Since the parents are R- and (by hypthesis) the triple mutant is R+, you have an easy selection. Are there other recombinant events that might produce R+ progeny? Don't be beguiled by the simplicity of this figure. Very few arrangements of the mutations lead to this result. To create the parental strains, you have to have a good knowledge of a genetic map of the mutations. That will be your primary task. Once you have a map with enough mutations on it, you'll be able to design and create the parents.

Figure 2: Recombination between two (-)(-)(+) mutants to produce (-)(-)(-) mutant.