Radiation exposure is a linear relationship.
Time and exposure are directly related.
The longer a person is exposed, the greater the amount of radiation received.
Therefore, the more efficient the technologist is when working in a radiation area the less he/she will receive.
Application of time and radiation exposure:
Calculation to the above statement:
(100mr/hr)/(60 minutes/1hr) = 1.67 mr/minute
30 minutes of exposure = 1.67 * 30 = 50 mr total exposure
15 minutes of exposure = 1.67 * 15 = 25 mr total exposure
Radiation exposure can be reduced by increase the distance from the source of radiation. This can be explained by the application of the inverse square law (see below):
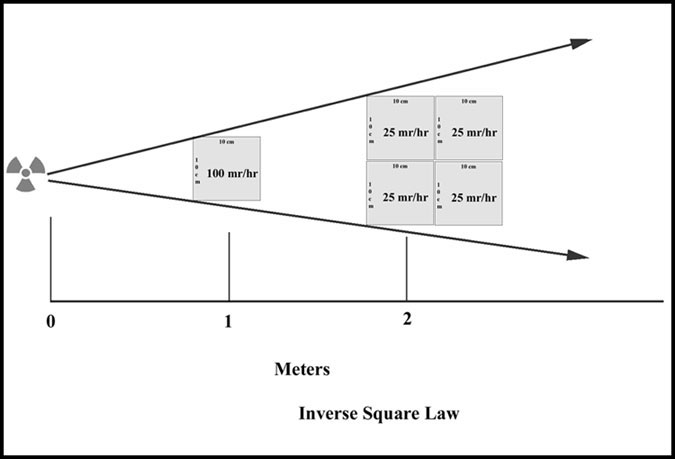
Inverse Square Law:
A source of radiation or intensity (I) at a distance (D) from a radioactive source has an "inverse square" relationship.
Example: At a distance (D) of 1 meter, a source of radiation (I) emits 100 mr/hr. If you increase the distance 1 meter to a distance of 2 meters, then the amount of radiation (i) decreases to 1/4 or 25 mr/hr. Applying the inverse square relationship shows that the new distance of 2 meters is first inverted to 1/2 and then squared 1/4. This results in a reduction of exposure to 1/4 of the original amount at 2 meter. Therefore, amount be emitted is reduced to 25 mr/hr when the distance is doubled.
Inverse Square Law Formula
I(D)2 = i(d)2
- Where I is the original amount of radiation and D is the original distance
- And where i is the new intensity and d is the new distance. The following calculation is applied:
I(D)2 = i(d)2(100 mr/hr) (1 meter)2 = (I) (2)2
25 mr/hr = I
Additional Example:
At one meter, Ted the Technologist reads that the activity level from a source is 40 mR/hr. What is the activity reading at 2 meters away from the source?
I = 40 mR/hr, D = 1 meter, d = 2 meters, i = ?
40 mR/hr * (1 m)2 = i * (2 m)2
40 mR(m)/hr = i * 4 m
10 mR/hr = i
Answer: The activity level at 2 meters from the source is 10 mR/hr.
Conclusion: Whenever possible, a technologist should increase his/her distance when working with a radiation source
3. Shielding
In order to attenuate a source of radiation, three factors must be considered:
- The density of the material being used to attenuate the radiation. The greater the density, the more attenuation or the greater the radiation is absorbed by the shield.
- The thickness of the attenuator is defined in half value layers (HVLs). For each HVL, the radiation is reduced by 50% exponentially. As an example
- Energy of the gamma radiation (keV). The greater the energy, the greater the density of the attenuator must be in order to have the same HVL effect.
Examples of how effective certain materials are with relation to energy gamma and density:
| Shield or Attenuator Density gm/cm3 |
Pb 11.34 |
Al 2.7 |
HVL of 140 keV |
0.0256 mm |
0.174 mm |
HVL at 364 keV |
0.219 mm |
2.646 mm |
HVL at 511 keV |
0.4021 mm |
3.094 mm |
From the above table one, can observe the relationship of the energy gamma to the required density of the attenuator. In general, shielding is adaquate if 10 HVLs is applying to a radiation source
If the energy gamma emits 140 keV a 100 mR/hr, what is the mR/hr after use of a lead shield that is 0.22 mm thick?

Answer: After adding the shielding, the source of radiation is reduced to 3.85 mR/hr.
Now it is time to apply all three aspects of radiation protection using the following example.
A source of radiation emits 1045mR/hr at 2.4m. The technologist shields the source that has a thickness of 1.9cm of lead. What is your radiation exposure is you stand 0.75m from the source for 37 minutes? (HVL of lead = 0.22cm)
Step 1. 1.9cm /0.22cm = 8.64 HVL
Step 2. 1045mR/hr / 28.64 = 2.62 mR/hr
Step 3. (2.62mR/hr) * (2.4m)2 = i * (0.75m)2
i = 26.95mR/hr at 0.75m
Step 4. 26.95mR/hr / 60min = 0.45mR/min
Step 5. (0.45mR/min) * (37 min) = 16.62mR
Answer: You receive an exposure of 16.62mR in 37 minutes at 0.75 meters from the source.
The decay formula is another application that we need to discuss.
Return to the beginning of the document
Return to the Table of Contents
5/22