- Attenuation of photons by the body habitus makes it difficult to obtain accurate quantitative information. If fact attenuation and scatter actually distorts the acquired data
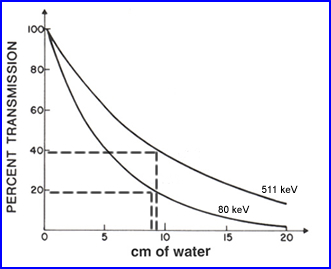
- As an example in PET brain <40% of the photon actually make it out of the cranium. The reason for this is the fact that gamma rays have to traval as much as 10 cm in a fluid media. This media attenuates and scattered the gamma radiation
- As a second example 133Xe is seen above and in this case approximately 20% of the gammas being emitted actually get outside the body after travel ing 10 cm of water
- This information tell us - as photon energy increases attenuation and scatter decreases. Consider this point how how it differs between SPECT and PET imaging
- Measuring/imaging hot spots with varying amounts of activity in different locations along the same rays is another issue (see above example)
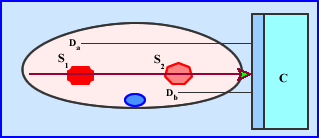
- C is the detector head collecting counts at a specific angle (ray)
- The hottest source of radiation is at the most extreme point, S1 and has a distance, Da, from C
- Another source of radiation is a lot closer to the camera, but is has less activity, S2 and its distance, Db, from C
- Considering the distances the attenuation is significantly greater with S1 when compared to S2
- Is there an issue with two sources at varying distances?
- What if S1 has significantly more activity when compared to S2? Does this affect the SPECT acquisition?
- Acquisition data become mixed with the varying degrees of activity and attenuation because SPECT has difficulty in defining the differences in activity. Hence this can effect quantitative issues
- Measurements of photons being attenuated as a function of distance
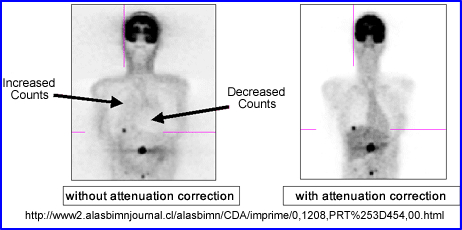
- The above image on the left defines activity without attenuation correction while the one on the right has attenuation correction. Profile and graft notes count distribution with both images
- What is interesting is that an image without attenuation correction shows significant loss of activity in the center of a homogenous volume of liquid. Additionally, the activity is more hotly distributed along the edge of the image
- What is the cause of this? This problem relates to the graph comparing the different energy gammas, specifically its an attenuation problem. The further away the activity has to travel the greater the amount of attenuation occurs, hence the center of the activity shows falsely reduce activity in its volume
- For this reason an attenuation coefficient (correction) must be applied to the reconstruction process which should improve image quality
- From a filtering standpoint this, application of an attenuation correction can be mathimatically, as long as the volume being imaged is homogenous, such as the brain
- Applying the right attenuation filter falsely raises the activity in the center hypothetically accounting for the attenuated gamma rays
- Attenuation correction can be applied either to raw data (Sorenson filter) or during the reconstruction process (Chang filter)
- Another term for these filters is first-order attenuation correction and should only be applied when there is homogenous uptake (liver/brain).
- An example of an incorrect appication would be the heart. Why? Consider the numerous surrounding structures with varying densities. This would require multiple attenuation coefficient applied only to areas that correlate to the appropriate density. Therefore, a coefficient approach to correct for attenuation becomes impossible.
- Furthermore low energy gammas emitters are not recommended for the first-order filters
- Consider cardiac imaging with the administration of 201Tl?
- In the case of imaging an organ or disease where there are multiple densities a transmission source is reocmmended which should correct for a heterogeneous densities
- Use of a transmission source can be done with either a radioactive rod source attached to a fan-beam collimator or with an x-ray tube (CT is the best example)
- Application of attenuation correction to non-homogeneous studies is therefore recommended. It will take care of the edge packing artifact that occurs along the outer rim of the reconstructed target. Therefore it is recommended that:
- Sorenson or Chang filters be applied to homogenous densitiies
- Transmission source be used with structures that have multiple densities

- The counts in SPECT reconstructed images are, in theory, directly proportional to the absolute concentration of radiopharmaceutical in the organ or organ system of interest (e.g., mCi/cc or MBq/cc)
- The 2 main factors that prevent SPECT from achieving a quantitative goal relates to gamma rays inside the body interact with attenuation and Compton scatter prior to exiting. These 2 phenomena cause spatial distortion of the measured amount of injected activity, hence effecting the ability to quantify the image
- Attenuation reduces the total amount of counts being collected
- Compton scatter reduces the amount of counts being collected
- Attenuation
- For a given concentration of radioactivity the relative number of gamma rays that escape the attenuating medium and those that are detected by the gamma camera can be determined by this equation:
- I = the attenuated intensity of gamma arrays
- Io is the gamma-array emission intensity without attenuation
- µ = the linear attenuation coefficient of the medium (for example, approximately 0.15 cm-1 for 99mTc in soft tissue)
- lq = the depth of the medium between the source of activity and the gamma camera at projection angle q
where:
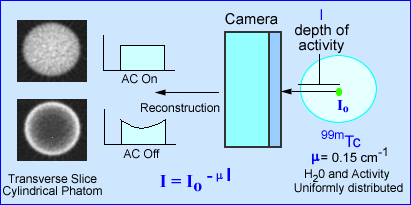
- The effects of attenuation on SPECT imaging is further noted in the above image. The intensity of photons emerging from a source (cylindrical phantom) of activity has a given amount of attenuation, water, that reduces the amount of gamma emission. The value e -µl, in the formula identifies µ as the linear attenuation coefficient in cm-1 and l as the depth of the activity in the attenuating medium. This is based on a specific projection
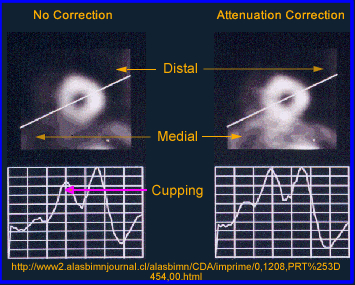
- When attenuation correction (AC) is off a cupping artifact in seen in tranverse reconstructed image. The explanation of the cold center occurs because of the attenuated gammas. If fact the closer to the center of the cylinder the greater attenuation. However, if AC is turned on the there is an equal distribution of actiivty accross the entire transbverse slice
- In SPECT studies dominated by soft tissue attenuation may required the application of, µ, which can be done by using a filter, such as Chang. A value of 0.15 cm-1 is applied since soft tissue attenuation has the same density as water
- When soft tissue is combine with air and/or bone (i.e. lungs) the attenuation phenomenon becomes too complicated to handle the attenuation from a mathematical standpoint. It is in this type of situation that a transmission scan is needed to account for the attenuation variations
- Attenuation correction methods may be categorized as:
- Constant µ, or the Chang method
- Variable µ, or transmission source method
- When the imaging media is at least somewhat uniform, the Chang filter is recommended. An attenuation map is based on the boundaries drawn around the patient skull were the constant µ is applied. This generated reconstructed transverse slices. ( µ = 0.15 cm-1)
- Now let is consider variable attenuation coefficient which is dependent on the spatial location of the pixel in the patient
- The quantitative value of µ is determined by the use of transmission scanning, either by use of a line sources , or x-ray transmission
- From the transmission scan, a µ map is generated, which is the inverse of the attenuation correction factor
- Transmission sources are long-lived radioisotopes that should have energies similar to the radioisotope being acquired. 153Gd (100 keV) maybe preferred for 201T while 57Co (122 and 136 keV) might be preferred with 99mTc. The correction factors are then converted to the attenuation coefficient map from the transmission data.
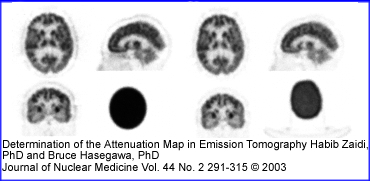
- In the above image the image on PET brain scan on the left uses a attenuation map generated from a single µ value. The image on the right uses a 137Cs source for its attenuation correction. Do you see a difference between both procedures? If so, where?
- The accuracy of the transmission source attenuation correction methods depends on the strength of the transmission source, lack of patient motion, and the attenuation correction algorithm itself
- Variable µ attenuation correction may be best performed using iterative reconstruction methodology, but can also applied to filtered backprojection.
- The clinical accuracy of transmission scanning methods in perfusion SPECT imaging is currently the subject of controversy. Attenuation correction has been shown to be of some use, but complete correction in all patient studies still eludes the technology
- From my own personal experience in nuclear cardiology (my opinion) is that variable attenuation correction does not greatly improve the diagnostic ability of the procedure. The problem may have been that motion correction could be applied to the emission data, could not be applied to the transmission (GE software). If the program now allows for motion correction of the transmission data my guess is that it might significantly improve this correction technique
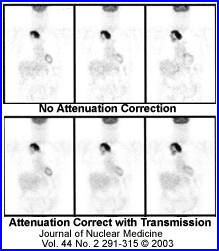
- Yet another example of the applicaiton of transmission data is seen in the above PET scan. What seems improved? Check the background activity. Check image resolution
- Compton Scatter
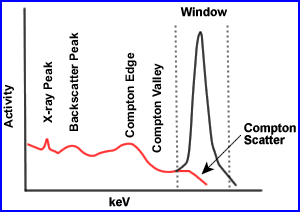
- The finite energy and spatial resolution of the SPECT imaging system allow for the acceptance of a certain amount of Compton scatter gamma rays (8 - 12%).
- The accepted scatter is dominated by narrow angle scattered gamma rays, which interact with orbital electrons and have energies slightly less than that of pure photopeak gamma rays, but are within lower end of the window. Note the red scatter line
- Compton scatter degrades resolution and acts as a modifier to the effective attenuation coefficients in a depth dependent fashion. Moreover, misplaced Compton scattered events adversely effect image contrast. Contrast is effected because false data is being accepted in the counting window
- Some SPECT systems include scatter correction methods based on the physics and probability of the Compton scatter process by using multiple or weighted energy window. An method to consider for Compton correction:
- Collect two separate photo peaks
- The first peak is set to the energy gamma (A) and the second is set to Compton peak (B)
- A - B = an energy peak with reduced Compton scatter
- In the future, improved energy resolution and window acquisition methods, and iterative reconstruction methods will include Compton scatter modeling
- Attenuation correct
- Filters have been designed to take attenuation into account
- The only problem with this approach is that the user can only apply this to areas of the body where the body habitus density remains relatively constant (brain and liver)
- Why should attenuation be taken into account? Remember the cupping artifact? Graphically the above example shows the affects of cupping in the LV of the myocardium. A profile is drawn through heart and a decreased in counts can be seen in the septal wall. Can you explain this artifact?
- The two types of attenuation filters are used in nuclear medicine: Chang (applied post reconstruction) and Sorenson (applied prior to reconstruction)
- The Chang method starts by drawing an ROI around the widest portion of the transverse slice. Once defined an attenuation value is then given to the data and a correction in counts is applied to the pixels inside the ROI. In theory this increases the counts coming from the center of the image negating the cupping artifact. Remember - the closer to the center of the brain (or any organ) the greater the gamma attenuation and the greater the need for correction
- Water has a µ value of 0.15 cm-1 which is applied to all liver brain and liver attenuation filters
- While attenuation correct filters are sometimes used to improve image quality this process cannot be done if there are different areas of density within the FOV. At this point only a transmission source can be used to compensate for the differences in density within the imaging media. Example of this would include the myocardium and bone
- Transmission imaging can be accomplished with the use of a line source and a fan beam collimator or with an x-ray tube (CT)
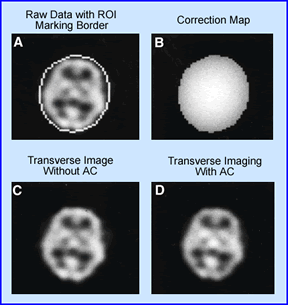
Chang post processing attenuation correction method is applied to the above image. (A) Shows the original uncorrected central transverse slice at a 128 x 128 matrix. This is a 99mTc-HMPAO brain SPECT study, were a boundary or "ROI" was drawn around the skull. (B) Is a correction map applied to the area inside the boundary and applied to all projections ( 0.15 cm-1). (C) Displays the uncorrected slice and (D) Represents the attenuation-corrected slice. Do you see any improvement? Look at the center of both images. Look at the edges. Remember this is were attenuation has its effect. To avoid under or over correction, the boundaries must be correctly defined. In some programs it RIOs are drawn automatically