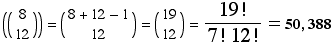| Discrete Structures |
Test #2
|
November 17 , 2003
|
| Name____________________ |
R. Hammack
|
Score ______
|
(1) Use induction to prove the following
statements.
(a) (10 points) If
n is a natural number, then 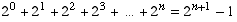 .
.
Proof.
Basis step. If n = 0, then the statement
is 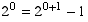 ,
which is just the (true) statement 1 = 1.
,
which is just the (true) statement 1 = 1.
Inductive step. Suppose k is a natural
number and the statement is true for n
= k.
This means 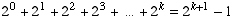 .
.
Now add 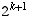 to
both sides to get:
to
both sides to get:
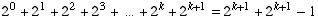
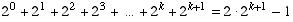
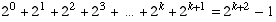
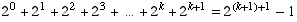 .
.
Thus the statement is true for k+1, so the theorem is proved. �
Note: Here is a simple non-inductive proof.
In binary form, 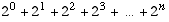 is just the n-digit binary number 1111111...111 consisting
of n ones.
is just the n-digit binary number 1111111...111 consisting
of n ones.
Any computer science student knows that this is 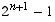 .
.
(b) (10 points) If
n is a natural number, then 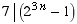 .
.
Proof.
Basis step. If n = 0, then the statement
is 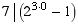 ,
which is just the (true) statement
,
which is just the (true) statement 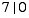 .
.
Inductive step. Suppose k is a natural
number and the statement is true for n
= k.
This means 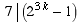 ,
so there is an integer c for which
,
so there is an integer c for which
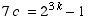 .
.
Hence 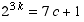 .
(This equation will be used in the next line.)
.
(This equation will be used in the next line.)
Now notice that 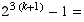
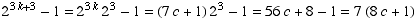 .
.
Thus we have determined that there is an integer 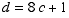 for
which
for
which 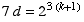 .
.
This means 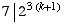 ,
and the statement for k+1 is true.
�
,
and the statement for k+1 is true.
�
(2) The questions on this
page are about the set 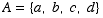 .
.
(a) (6 points) How
many different relations are there on A?
A relation is just a subset of 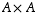 ,
so the question is the same as aking how many subsets of
,
so the question is the same as aking how many subsets of 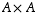 there are.
there are.
Answer: 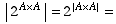
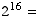 65,536
65,536
(b) (6 points) How
many different equivalence relations are there on A?
This is the same as asking how many partitions there are on A,
for the parts of a partition correspond to equivalence classes of an
equivalence relation. It's not hard to list all partitions of A.
| {{a}, {b}, {c}, {d}} |
{{a, b}, {c}, {d}} |
{{a, b}, {c, d}} |
{{a, b, c}, {d}} |
| |
{{a, c}, {b}, {d}} |
{{a, c}, {b, d}} |
{{a, b, d}, {c}} |
| |
{{a, d}, {b}, {c}} |
{{a, d}, {b, c}} |
{{a, c, d}, {b}} |
| |
{{b, c}, {a}, {d}} |
|
{{b, c, d}, {a}} |
| |
{{b, d}, {a}, {c}} |
|
|
| |
{{c, d}, {a}, {b}} |
|
{a, b, c, d} |
Answer: There are 15 equivalence relations.
(c) (6 points) How many different functions 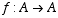 are there that satisfy
are there that satisfy 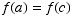 ?
?
(4)(4)(1)(4) = 64
(d) (6 points) How many different functions 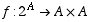 are there?
are there?
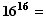 18,446,744,073,709,551,616
18,446,744,073,709,551,616
(e) (6 points) How many different injective functions 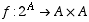 are there?
are there?
16! = 20,922,789,888,000
(3) The problems on this page concern length-6 lists made from the letters A, B, C, D, with repetition allowed.
(a) (6 points) How many such lists contain exactly 3 A's?
There are 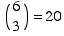 ways to choose the positions of the 3 A's.
ways to choose the positions of the 3 A's.
Then there are 3 slots left and you have 3 choices for each, so 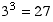 ways to fill them in.
ways to fill them in.
By the multiplication principle, there are (20)(27) = 540 such lists.
(b) (6 points) How many such lists contain exactly 3 A's and 1 B?
There are 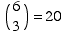 ways to choose the positions of the 3 A's.
ways to choose the positions of the 3 A's.
Then there are 3 slots left and you have 3 choices for where to put the B (3 ways to do this).
Finally there are 2 slots left and you have 2 choices for each. There are (2)(2) = 4 ways to fill them in.
By the multiplication principle, there are (20)(3)(4) = 240 such lists.
(c) (6 points) How many such lists are in alphabetical order?
Such a list could be encoded in stars-and-bars form.
Examples:
AABCCD ----> **|*|**|*
BBBCDD ----> |***|*|**
CCCCCC ---> ||******|
Thus the number of such lists is
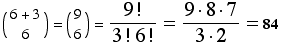
(d) (6 points) How many such lists are not in alphabetical order?
There are 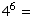 4096 lists all together.
4096 lists all together.
As above, only 84 are in alphabetical order.
Thus 4096 - 84 = 4012 are not in alphabetical order.
(e) (6 points) How many such lists are there if the first, second, or third entry must be an A?
Let A be the set of lists of form A _ _ _ _ _ , and so 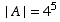
Let B be the set of lists of form _ A _ _ _ _ , and so 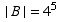
Let C be the set of lists of form _ _ A _ _ _ , and so 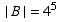
So 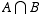 is all the lists of form A A _ _ _ _ , and so
is all the lists of form A A _ _ _ _ , and so 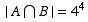
So 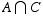 is all the lists of form A _ A _ _ _ , and so
is all the lists of form A _ A _ _ _ , and so 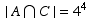
So 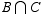 is all the lists of form _ A A _ _ _ , and so
is all the lists of form _ A A _ _ _ , and so 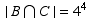
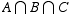 is the lists of form A A A _ _ _ , and so
is the lists of form A A A _ _ _ , and so 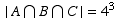
By the inclusion-exclusion formula, the answer is
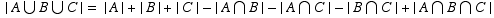
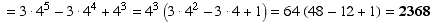
Here's another way of looking at it.
(# of lists with 1st 2nd or 3rd element A) = (total # of lists) - (# of lists with 1st 2nd and 3rd element NOT A)
= (4)(4)(4)(4)(4)(4) - (3)(3)(3)(4)(4)(4) = 2368
The number of lists where the first, second or third element is NOT an A is (3)(3)(3)(4)(4)(4)
then the
(4)
(a) (5 points) Find the coefficient of 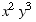 in the expansion of
in the expansion of 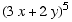 .
.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Looking at Pascal's Triangle, and applying the Binomial Theorem,
you can see that the relevant term is 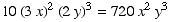 .
.
Answer: 720
(b) (5 points) How many anagrams of the word BANANA are there?
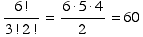
(c) (5 points) In how many ways can a group of 12 people be divided into 3 teams of 4 each? (In this problem, the teams are distinct. Call them Team A, Team B, and Team C.)
First choose 4 out of 12 people for Team A. There are 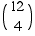 ways of doing this.
ways of doing this.
Next, there are 8 people left. Choose 4 of them for Team B. There are 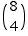 ways of doing this.
ways of doing this.
This leaves 4 people unchosen. Put them on Team C.
By the multiplication principle, the total number of ways to choose the teams is
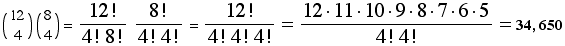 different ways.
different ways.
(d) (5 points) A coffee shop sells 8 different kinds of bagels. How many ways are there to order a dozen bagels?