| Linear Algebra |
Test #2
|
May 5, 2003
|
| Name____________________ |
R. Hammack
|
Score ______
|
(1) This problem concerns the matrix 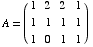 .
.
(a) Is 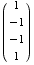 in the null space of A?
in the null space of A? 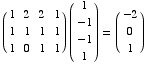 ,
so the answer is NO
,
so the answer is NO
(b) Is [2 9 7 2] in the row
space of A?
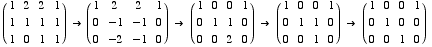
Now you can see that Row(A) = Span( [1 0 0 1], [0 1 0 0], [0 0 1 0] ).
Then [2 9 7 2] = 2[1 0 0 1] +
9[0 1 0 0] + 7[0 0 1 0] is in Row(A).
So the answer to the question is YES.
(2) 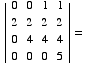
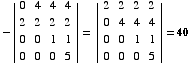
(3) Find the inverse of this matrix without doing any row reductions. (Hint:
is it orthogonal?) ![(1 1 1 ) - -- ------- 2 2 ... 1 - - ------- 2 2 0 Sqrt[2]](HTMLFiles/T2S03Asol_7.gif)
It's orthogonal, so its inverse is its transpose: ![(1 1 1 1 ) - - - - 2 2 ... 1 1 -------- ------- 0 0 Sqrt[2] Sqrt[2]](HTMLFiles/T2S03Asol_8.gif)
(4) Suppose 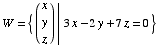 . Find
. Find
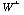 .
.
Note that W is the plane orthogonal to 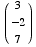 ,
so
,
so 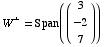 .
.
(5) Consider the matrix 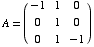
(a) Find the eigenvalues of A.
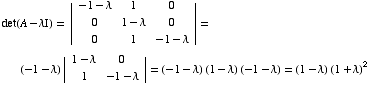
Eigenvlaues are -1 and 1.
(b) Find the eigenspaces of A.
To find the eigenvectors for 1: Compute Null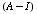
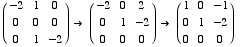
x = z
y = 2z
z = free
Eigenspace: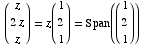
To find the eigenvectors for -1: Compute Null(A + I)
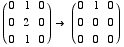
x = free
y = 0
z = free
Eigenspace: 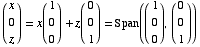
(c) Diagonalize the matrix A, that is find an invertible matrix P and a diagonal matrix D with 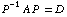 .
.
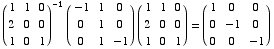
(6) Suppose 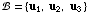 is
an orthogonal basis for
is
an orthogonal basis for 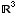 having
the property that
having
the property that 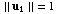 ,
,
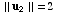 ,
and
,
and 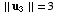 .
Suppose also that
.
Suppose also that 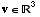 satisfies
satisfies
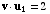 ,
, 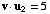 ,
and
,
and 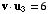 .
Find
.
Find ![[v] _ !,](HTMLFiles/T2S03Asol_31.gif) .
.
Notice that:
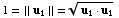 ,
so
,
so 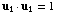
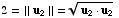 ,
so
,
so 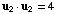
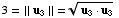 ,
so
,
so 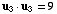
Now since the basis is orthogonal, ![[v] _ !, = (v · u ) = (2) = ( ) 1 - ------------ ... 3 -------------- u · u 3 3](HTMLFiles/T2S03Asol_38.gif)
(7) Suppose 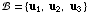 is
a basis for
is
a basis for 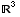 , and
, and 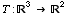 is a linear transformation for which
is a linear transformation for which 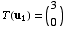 ,
, 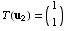 ,
and
,
and 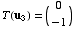 .
Moreover, suppose v is a vector in
.
Moreover, suppose v is a vector in 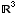 for
which
for
which ![FormBox[RowBox[{v, =, Cell[TextData[{3, Cell[BoxData[u ]], +2, Cell[BoxData[u ]], +5, Cell[Box ... 1 2 3](HTMLFiles/T2S03Asol_46.gif) . Find
T(v).
. Find
T(v).
![FormBox[RowBox[{T(v), , =, , RowBox[{RowBox[{T, (, Cell[TextData[{3, Cell[BoxData[u ]], +2, ... 0 1 -1 -3](HTMLFiles/T2S03Asol_47.gif)
(8) Suppose A is a matrix which has 5 rows, and the rows are linearly
independent. Suppose also that Null(A) is two-dimensional. How many columns
does A have?
Since the rows are linearly independent, the 5 rows form a basis for the row
space.
Thus rank(A) = dim(Row(A)) = 5.
By Rank Theorem: Rank(A) + Nullity(A) = n = (number of
columns)
Thus (number of columns) = 5 + 2 = 7
(9) Suppose A is a 5×5 matrix with a one-dimensional null
space. Find det(A).
Since the null space is one dimensional, it follows that Null(A) = span(x)
for some nonzero vector x.
This means that Nullity(A) = 1. Since Nullity(A) is not zero,
A is not invertible, by the invertible matrix theorem. Hence det(A)
= 0.
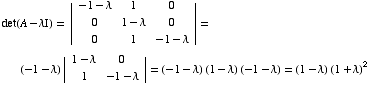
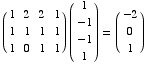 ,
so the answer is NO
,
so the answer is NO
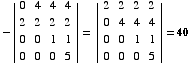
![(1 1 1 ) - -- ------- 2 2 ... 1 - - ------- 2 2 0 Sqrt[2]](HTMLFiles/T2S03Asol_7.gif)
![(1 1 1 1 ) - - - - 2 2 ... 1 1 -------- ------- 0 0 Sqrt[2] Sqrt[2]](HTMLFiles/T2S03Asol_8.gif)
![[v] _ !, = (v · u ) = (2) = ( ) 1 - ------------ ... 3 -------------- u · u 3 3](HTMLFiles/T2S03Asol_38.gif)