(1) This problem concerns the matrix
(a) Is
(b) Is [2 9 7 2] in the row space of A?
| Linear Algebra |
Test #2
|
May 5, 2003
|
| Name____________________ |
R. Hammack
|
Score ______
|
(1) This problem concerns the matrix ![]() .
.
(a) Is ![]() in the null space of A?
in the null space of A?
(b) Is [2 9 7 2] in the row
space of A?
(2) 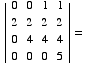
(3) Find the inverse of this matrix without doing any row reductions.
(Hint: is it orthogonal?) ![(1 1 1 ) - -- ------- 2 2 ... 1 - - ------- 2 2 0 Sqrt[2]](HTMLFiles/T2S03Asol_7.gif)
(4) Suppose ![]() . Find
. Find
![]() .
.
(5) Consider the matrix ![]()
(a) Find the eigenvalues of A.
(b) Find the eigenspaces of A.
(c) Diagonalize the matrix A, that is find an invertible matrix
P and a diagonal matrix D with ![]() .
.
(6) Suppose ![]() is
an orthogonal basis for
is
an orthogonal basis for ![]() having
the property that
having
the property that ![]() ,
,
![]() ,
and
,
and ![]() .
Suppose also that
.
Suppose also that ![]() satisfies
satisfies
![]() ,
, ![]() ,
and
,
and ![]() .
Find
.
Find ![]() .
.
(7) Suppose ![]() is
a basis for
is
a basis for ![]() , and
, and ![]() is a linear transformation for which
is a linear transformation for which ![]() ,
, ![]() ,
and
,
and ![]() .
Moreover, suppose v is a vector in
.
Moreover, suppose v is a vector in ![]() for
which
for
which ![]() . Find
T(v).
. Find
T(v).
(8) Suppose A is a matrix which has 5 rows, and the rows are linearly
independent. Suppose also that Null(A) is two-dimensional. How many columns
does A have?
(9) Suppose A is a 5×5 matrix with a one-dimensional null
space. Find det(A).![]()