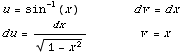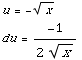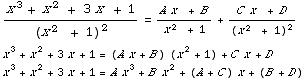___________________________________________________________________
Calculus II Test
#3 April
15, 2005
Name____________________ R. Hammack Score
______
___________________________________________________________________
(1) ∫ 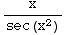 dx
=
dx
= 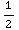 ∫ cos(
∫ cos(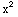 )2x
dx
=
)2x
dx
= 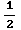 sin(
sin(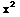 )
+ C
)
+ C
(2) ∫ x
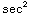 (x) dx
= x tan(x)-∫ tan(x) dx
= x tan(x)-ln| sec(x) | + C
(x) dx
= x tan(x)-∫ tan(x) dx
= x tan(x)-ln| sec(x) | + C
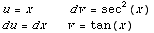
(3) ∫
sec(x) dx
= ln| sec(x) + tan(x) | + C
(4) 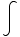
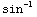 (x)dx
=
(x)dx
=
x 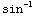 (x)
-
(x)
- 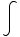 x
x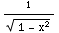 dx
=
dx
=
x 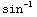 (x)
+
(x)
+ 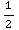
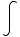
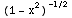 (-2x
) dx
=
(-2x
) dx
=
x 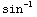 (x)
+
(x)
+ 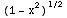 +
C =
+
C =
x  (x)
+
(x)
+ 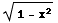 +
C
+
C
(Using interation by parts with the following
substitutions:)
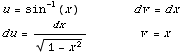
(5) ∫ 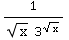 dx
= -2∫
dx
= -2∫ 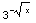
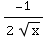 dx
= -2∫
dx
= -2∫ 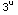 du
=
du
=
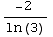
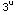 + C =
+ C = 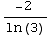
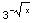 + C =
+ C =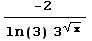 +
C
+
C
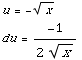
(6) ∫
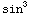 (x)
(x)
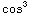 (x)
dx
= ∫
(x)
dx
= ∫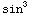 (x)
(x)
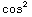 (x)cos(x)
dx
=
(x)cos(x)
dx
=
∫ 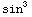 (x)
(1-
(x)
(1-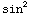 (x))cos(x)
dx
= ∫
(x))cos(x)
dx
= ∫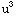 (1-
(1-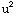 )du
=∫
)du
=∫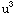 -
-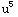 du
=
du
=
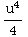 -
-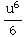 +C=
+C=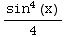 -
-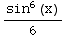 +
C
+
C
(7) ∫ 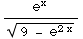 dx
= ∫
dx
= ∫ 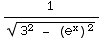
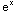 dx
=
dx
=
∫ 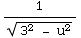 du
=
du
=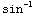 (
(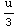 )
+ C =
)
+ C =  (
(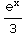 )
+ C
)
+ C
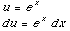
(8) 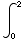
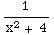 dx
=
dx
= 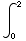
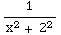 dx
=
dx
= ![[1/2tan^(-1)(x/2)] _0^2](HTMLFiles/T3S05D_59.gif) =
= 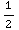
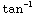 (1)
=
(1)
=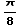
(9) ∫
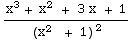 dx
= ∫
dx
= ∫
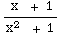 +
+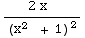 dx
=
dx
=
∫
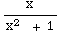 dx
+ ∫
dx
+ ∫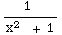 dx
+ ∫
dx
+ ∫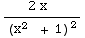 dx
=
dx
=
=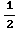 ln(
ln(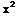 +2)
+
+2)
+  (x)
-
(x)
-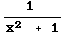 +
C
+
C
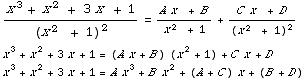
A =1
B =1
C = 2
D = 0
(10) ∫
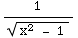 dx
=∫
dx
=∫ 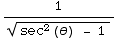 sec(θ)tan(θ) dx
=
sec(θ)tan(θ) dx
=
∫ 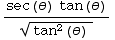 dx
= ∫sec(θ)
dx
= ln| sec(θ) + tan(θ) | + C
dx
= ∫sec(θ)
dx
= ln| sec(θ) + tan(θ) | + C
=ln| x+tan(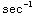 (x))
|+C=ln| x +
(x))
|+C=ln| x +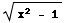 |
+ C
|
+ C
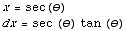
(11) 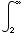
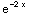 dx
=
dx
=
![Underscript[lim , l∞]](HTMLFiles/T3S05D_82.gif)
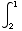
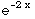 dx =
dx =![Underscript[lim , l∞][-e^(-2x) /2] _2^l](HTMLFiles/T3S05D_85.gif) =
=![Underscript[lim , l∞][-1 /(2e^(2x))] _2^l](HTMLFiles/T3S05D_86.gif) =
=
![Underscript[lim , l∞]](HTMLFiles/T3S05D_87.gif) (-
(-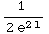 +
+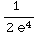 )
= 0 +
)
= 0 + 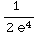 =
= 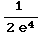
(12) 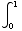
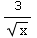 dx
=
dx
=
(Note: The integral is improper)
=![Underscript[lim , l0^+]](HTMLFiles/T3S05D_94.gif)
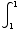 3
3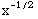 dx =
dx = ![Underscript[lim , l0^+][3x^(1/2)/(1/2)] _l^1](HTMLFiles/T3S05D_97.gif) =
= ![Underscript[lim , l0^+][6x^(1/2)] _l^1](HTMLFiles/T3S05D_98.gif) =
= ![Underscript[lim , l0^+]](HTMLFiles/T3S05D_99.gif) (6
(6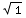 -6
-6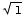 )
= 6
)
= 6
(13) ![Underscript[lim , x⟶1]](HTMLFiles/T3S05D_102.gif)
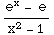 =
= ![Underscript[lim , x⟶1]](HTMLFiles/T3S05D_104.gif)
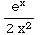 =
= 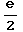
(14) ![Underscript[lim , x⟶∞]](HTMLFiles/T3S05D_107.gif) x
x
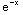 =
=![Underscript[lim , x⟶∞]](HTMLFiles/T3S05D_109.gif)
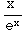 =
=![Underscript[lim , x⟶∞]](HTMLFiles/T3S05D_111.gif)
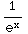 = 0
= 0