Calculus II Test #2 March 18, 2005
Name____________________ R. Hammack Score ______
______________________________________________________________________
(1) Find the area of the region contained between the graphs of y=
![∫_ (-1)^2 (x^2 + 1 - x) dx =[x^3/3 + x - x^2/2] _ (-1)^2 = (2^3/3 + 2 - 2^2/2) - ((-1)^3/3 + (-1) - (-1)^2/2) = 8/3 + 2 - 2 + 1/3 + 1 + 1/2 = 9/2Square units](HTMLFiles/T2S05D_2.gif)
![[Graphics:HTMLFiles/T2S05D_3.gif]](HTMLFiles/T2S05D_3.gif)
_______________________________________________________________________
Calculus II Test
#2 March
18, 2005
Name____________________ R. Hammack Score
______
______________________________________________________________________
(1) Find the area of the region contained
between the graphs of y=![]() +1 and
y=x, and between x=-1 and x=2.
+1 and
y=x, and between x=-1 and x=2.
![∫_ (-1)^2 (x^2 + 1 - x) dx =[x^3/3 + x - x^2/2] _ (-1)^2 = (2^3/3 + 2 - 2^2/2) - ((-1)^3/3 + (-1) - (-1)^2/2) = 8/3 + 2 - 2 + 1/3 + 1 + 1/2 = 9/2Square units](HTMLFiles/T2S05D_2.gif)
![[Graphics:HTMLFiles/T2S05D_3.gif]](HTMLFiles/T2S05D_3.gif)
(2) Find the area of
the region contained between the curves y =![]() and y =
and y =![]() .
.
These curves intersect at points with x
coordinates that satisfy ![]() =
=![]()
![[Graphics:HTMLFiles/T2S05D_10.gif]](HTMLFiles/T2S05D_10.gif)
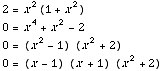
Thus, the curves intersect at x = 1
and x = -1.
![∫_ (-1)^1 (1/(1 + x^2) - x^2/2) dx =[tan^(-1) (x) - x^3/6] _ (-1)^1 = (tan^(-1) (1) - ... an^(-1) (-1) - (-1)^3/6) = π/4 - 1/6 + π/4 - 1/6 = π/2 - 1/3Square units](HTMLFiles/T2S05D_9.gif)
(3) Consider the region
contained between the graphs of y=![]() , y=0,
x=0, and x=π/3,
, y=0,
x=0, and x=π/3,
This region is revolved around the x-axis.
Find the volume of the resulting solid.
By slicing:
![∫_0^(π/3) πcos(x)^(1/2)^2dx = π∫_0^(π/3) cos(x) dx = π[ sin(x) ] _0^(π/3) = π ( sin(π/3) - sin(0)) = (π3^(1/2))/2Cubic Units .](HTMLFiles/T2S05D_12.gif)
![[Graphics:HTMLFiles/T2S05D_13.gif]](HTMLFiles/T2S05D_13.gif)
(4) Consider the region
contained between the graphs of y=![]() -2
-2![]() +x and y=0.
+x and y=0.
This region is revolved around the y-axis.
Find the volume of the resulting solid.
Note y = ![]() -2
-2![]() +x
= x(
+x
= x(![]() -2x+1)
=
-2x+1)
= ![]() ,
so the x intercepts are 0 and 1.
,
so the x intercepts are 0 and 1.
Drawing a rough sketch of the graph, we see that the region lies between 0 and
1 on the x-axis![[Graphics:HTMLFiles/T2S05D_20.gif]](HTMLFiles/T2S05D_20.gif)
Volume by shells:
![]() 2π
x(
2π
x(![]() -2
-2![]() +x)dx
= 2π
+x)dx
= 2π![]() (
(![]() -2
-2![]() +
+![]() )dx
= 2
)dx
= 2![]() = 2π(
= 2π( ![]() -
-![]() +
+![]() )
= 2π(
)
= 2π( ![]() -
-![]() +
+![]() )
=
)
= ![]() Cubic Units
Cubic Units
(5) Find the exact arc length of the curve y = f(x)
= ![]()
![]() dt between
x=1 and x=2.
dt between
x=1 and x=2.
Note: f'(x)=![]() . Now using the arc length formula, we get
. Now using the arc length formula, we get
![]()
![]() dx
=
dx
= ![]()
![]() dx
=
dx
= ![]()
![]() dx
=
dx
= ![]()
![]() dx=
dx=![]() (1+x)dx
=
(1+x)dx
= ![]() = (2+
= (2+![]() )-(1+
)-(1+![]() )
= 2+2-1-1/2 = 5/2 Units.
)
= 2+2-1-1/2 = 5/2 Units.
(6) Consider the graph of y=![]() +1 between x=1 and x=3. This graph is revolved around the x-axis. Find the area of the resulting surface.
+1 between x=1 and x=3. This graph is revolved around the x-axis. Find the area of the resulting surface.
Using the arc length formula, we get
![]() 2π(
2π(![]() +1)
+1)![]() dx
= 2π
dx
= 2π![]() (
(![]() +1)
+1)![]() dx
= π
dx
= π![]()
![]() (
(![]() +1)dx
= π
+1)dx
= π![]() = π
= π![]() ((
((![]() +3)-(
+3)-(![]() +1))
= π
+1))
= π![]() (
(![]() +3-
+3-![]() -1)
= 4π
-1)
= 4π![]() Square
Units.
Square
Units.
(7) A variable force
pushes an object 10 feet along a straight line in such a way that when the object
is x feet from its starting point,
the force on the object is 2-![]() pounds. How much work is done in moving the object 10 feet?
pounds. How much work is done in moving the object 10 feet?
Work =![]() ( 2-
( 2-![]() )dx
=
)dx
= ![]() = (20+
= (20+![]() )-(0+
)-(0+![]() )
= 10 Foot
pounds
)
= 10 Foot
pounds