_________________________________________________________________________________
Calculus II Test #1 March 4, 2005
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Find the following antiderivatives.
(a) ∫( 3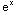 +
+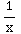 +ln(3) )dx = 3
+ln(3) )dx = 3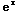 +ln|x|+x ln(3)+C
+ln|x|+x ln(3)+C
(b) ∫ x 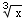 dx = ∫ x
dx = ∫ x 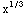 dx =∫
dx =∫ 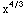 dx =
dx =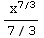 +C =
+C =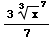 +C
+C
(c) ∫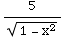 dx =5
dx =5  (x)+C
(x)+C
(d) ∫( 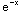 +sin(π x) + sec(x)tan(x) )dx = -
+sin(π x) + sec(x)tan(x) )dx = -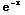 -
- 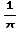 cos(π x) + sec(x)+C
cos(π x) + sec(x)+C
(e) ∫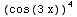 sin(3x) dx =
sin(3x) dx =
-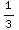 ∫
∫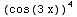 (-1)sin(3x)3 dx =-
(-1)sin(3x)3 dx =-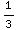 ∫
∫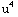 du =-
du =-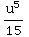 +C=-
+C=-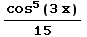 +C
+C
u = cos(3x) dx
du = -sin(3x)3 dx
(f) ∫x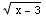 dx =
dx =
∫(u+3)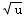 du =∫(
du =∫(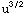 +3
+3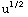 )du =
)du =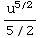 +3
+3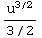 +C=
+C=
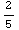
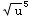 +2
+2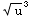 +C=
+C=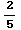
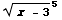 +2
+2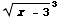 +C
+C
u = x - 3
du = dx
(2) Find the following definite integrals. Simplify your answer as much as possible.
(a) 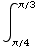
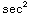 (x) dx =tan(π/3)-tan(π/4)=
(x) dx =tan(π/3)-tan(π/4)=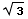 -1
-1
(b) 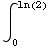 3
3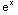 dx =3
dx =3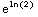 -3
-3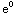 =6-3=3
=6-3=3
(c) 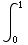 (
(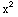 +x-1)dx =
+x-1)dx =![[x^3/3 + x^2/2 - x] _0^1](HTMLFiles/T1S05D_42.gif) =
=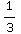 +
+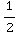 -1=-
-1=-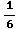
(d) 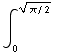 cos (
cos (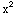 ) 2x dx =
) 2x dx =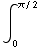 cos (u) du =sin (π/2)-sin (0)=1
cos (u) du =sin (π/2)-sin (0)=1
u = 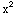
du = 2x dx
(e) 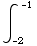
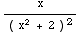 dx =
dx =
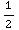
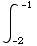
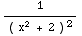 2x dx =
2x dx =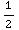
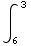
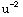 du =
du =![1/2[-1/u] _6^3](HTMLFiles/T1S05D_58.gif) =
=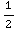 (-
(-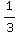 +
+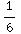 )=-
)=-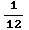
u = 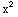 +2
+2
du = 2x dx
(f) 
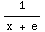 dx =
dx = 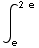
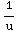 du =
du =![[ ln | u | ] _e^(2e)](HTMLFiles/T1S05D_68.gif) =ln|2e|- ln|e|=ln(2)+ln(e)-ln(e)=ln(2)
=ln|2e|- ln|e|=ln(2)+ln(e)-ln(e)=ln(2)
u = x +e
du = dx
(3) Consider the limit of Riemann sums ![Underscript[lim , max Δx_k0]](HTMLFiles/T1S05D_69.gif)
![Underoverscript[∑ , k = 1, arg3]](HTMLFiles/T1S05D_70.gif) (
(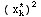 +1)Δ
+1)Δ 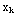 , where a=1 and b=2.
, where a=1 and b=2.
Find the value of this limit by writing it as a definite integral and evaluating.
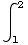 (
(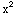 +1)dx =
+1)dx =![[x^3/3 + x] _1^2](HTMLFiles/T1S05D_75.gif) =(
=(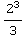 +2)-(
+2)-(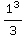 +1)=
+1)=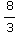 +2-
+2-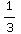 -1=
-1=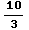
(4) Suppose a particle moving on the number line has a velocity of v(t)=t-1 units per second at time t.
(a) Find the object's displacement between times t = 0 and t = 4.
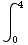 (t-1)dt =
(t-1)dt =![[t^2/2 - t] _0^4](HTMLFiles/T1S05D_82.gif) =
=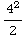 -4=4 units
-4=4 units
(b) Find the total distance the object has traveled between times t = 0 and t = 4.
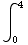 |t-1|dt =
|t-1|dt =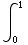 |t-1|dt +
|t-1|dt +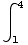 |t-1|dt =
|t-1|dt =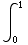 (1-t)dt +
(1-t)dt +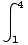 (t-1)dt=
(t-1)dt=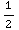 +
+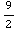 =5units
=5units
(5) This question concerns the function F(x)=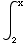
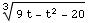 dt.
dt.
(a) F '(x)= 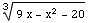
(b) Find the interval(s) on which F(x) increases.
F '(x)= 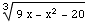 =
=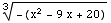 =-
=-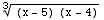
From this you can see the derivative is positive on the interval [4,5], so that is where F increases.
(6) Find the area of the region contained between the x-axis and the graph of y=1-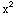 .
.
y=1-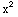 =(1-x)(1+x), so the x-intercepts are 1 and -1.
=(1-x)(1+x), so the x-intercepts are 1 and -1.
![[Graphics:HTMLFiles/T1S05D_99.gif]](HTMLFiles/T1S05D_99.gif)
Area = (1-
(1-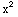 )dx =
)dx =![[x - x^3/3] _ (-1)^1](HTMLFiles/T1S05D_102.gif) =(1-
=(1-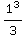 )-(-1-
)-(-1-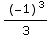 )=2-
)=2-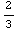 =
=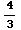 square units
square units
|
(7) Suppose
f(x) ={
|
2 if
x <0 |
| 2-x if x≥0 |
(a) Find 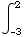 f(x)dx . (Suggestion: Sketch the graph of f.)
f(x)dx . (Suggestion: Sketch the graph of f.)
![[Graphics:HTMLFiles/T1S05D_108.gif]](HTMLFiles/T1S05D_108.gif)
Integral equals area of a 3 by 2 rectangle plus area of triangle of height and base 2.
Thus its value is (3)(2)+1/2(2)(2) = 8
(b) Find a value of x, different from -3, for which 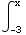 f(x)dx = 0
f(x)dx = 0
Notice that from the graph, if x = 6, the net signed area is 0. Hence the answer is x = 6.
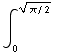
![[Graphics:HTMLFiles/T1S05D_99.gif]](HTMLFiles/T1S05D_99.gif)
![[Graphics:HTMLFiles/T1S05D_108.gif]](HTMLFiles/T1S05D_108.gif)