Calculus II Quiz #9 May 9, 2005
Name_________________ R. Hammack Score ______
___________________________________________________________
(1) Find the interval of convergence of the power series
Using the ratio test for absolute convergence, we get
ρ=
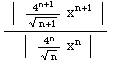 =
=For convergence, we need ρ=4|x|<1, so |x| < 1/4, or -1/4 < x < 1/4.
Check endpoint x = 1/4
Check endpoint x = -1/4
Conclusion: The interval of convergence is [-