Calculus II Quiz #8 April 29, 2005
Name_________________ R. Hammack Score ______
___________________________________________________________
Decide if the following series converge or diverge. In the case of convergence, say whether the series converges conditionally or absolutely.
(1)
For k > 1, the series has positive terms.
Further,
Therefore, the series converges by comparison with the convergent p-series
Since it converges and its terms are all positive, then it also converges absolutely.
(2)
Using the ratio test
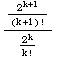 =
=Therefore the series converges. Since the terms are positive, it converges absolutely
(3)
This is an alternating series, with
Therefore it converges by the alternating series test.
However,
Therefore the original series converges conditionally.
(4)
Note that
Therefore the series diverges by the divergence test.