Calculus II Quiz #7 April 22, 2005
Name_________________ R. Hammack Score ______
___________________________________________________________
(1) Decide if the following sequences converge or diverge. In the case of convergence, state the limit if it can be determined.
(a)
(b)
Odd terms approach -
(c) (
The nth term is
(d)
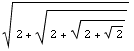 ,
...
,
...Note: The series is defined recursively as
If the sequence has a limit L, then L =
which gives L =
Thus
(L - 2)(L + 1) = 0
So L is either 2 or -1.
But the series has positive terms, so it couldn't converge to a negative number.
Thus, if it converges, it must converge to 2.
But does it converge?
From its definition, it should be clear that the sequence is increasing.
Also, notice that it has 2 is an upper bound, for:
Thus, it is an increasing sequence that is bounded above.
Therefore must converge, and as computed above, it converges to 2.