Calculus II Test #3 April 19, 2004
Name____________________ R. Hammack Score ______
___________________________________________________________________
(1) Find the following integrals.
(a)
(b)
(c)
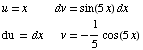
(d)
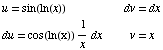
Now we use integration by parts a second time on the most recent integral.
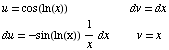
Plugging THIS back into the first line gives
From this we get
so
(e)
(f)
(g)
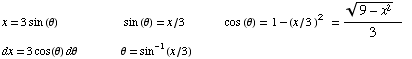
Converting the above expression back to x, we get:
(h)
(i)
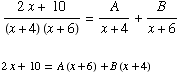
Set x = -6, get 2(-6)+10 = -2B ====> B=1
Set x = -4, get 2(-4)+10 = 2A ====> A=1
(j)
Doing the long division:
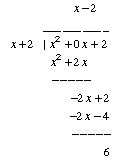
Therefore
(2) Evaluate the following improper integrals.
(a)
(b)
![Underscript[lim , l0^+] ∫_l^1x^(-1/3) dx = Underscript[lim , l0^+][(x^(1/3))^2/(2/3)] _l^1 = Underscript[lim , l0^+] ((1^(1/3))^2/(2/3) - (l^(1/3))^2/(2/3)) = 3/2](HTMLFiles/T3S04Hsol_36.gif)
(3) Evaluate the limits.
(a)
(b)
![Underscript[lim , x⟶∞] e^ln((1 - 3/x)^x) = Underscript[lim , xϿ ... ^2/(1 - 3/x)/(-1/x^2)) = e^( Underscript[lim , x⟶∞] -3/(1 - 3/x)) = e^(-3)](HTMLFiles/T3S04Hsol_40.gif)