Calculus II Test #1 March 3, 2004
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Find the following antiderivatives.
(a)
(b)
(c)
(d)
(e)
(f)
(2) Use Part 2 of the Fundamental Theorem of Calculus to write an antiderivative of
(3) Find the following definite integrals. (You may use any technique. Sometimes area may be the best approach.)
(a)
(b)
(c)
(d)
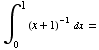
(e)
(f)
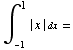
(4) Use the definition of the definite integral to write
(You do not need to find the value of this integral -- just write down the limit,)