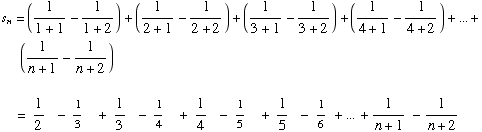___________________________________________________________
Calculus  II                                           Quiz #9                     April 27, 2003

Name_________________            R.  Hammack                  Score ______
___________________________________________________________
Decide if the following series converge or diverge. In the case of convergence, state the sum.

(1)   Underoverscript[∑ , k = 0, arg3] (-1)^k5/3^k = Underoverscript[∑ , k = 0, arg3] 5 (-1/3)^k = 5/(1 - -1/3) = 5/4/3 = 15/4
  (Geometric series, a = 5,  r = -1/3, so it converges since |r| < 1.)


(2)  Underoverscript[∑ , k = 0, arg3] (5/3)^k   DIVERGES
(Geometric series, a = 1,  r = 5/3 > 1, so it DIVERGES)


(3)    Underoverscript[∑ , k = 1, arg3] 1/(k + 1 )= 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 +...  DIVERGES
(Harmonic series, minus first term.)

(4)   Underoverscript[∑ , k = 1, arg3] 1/((k + 1) (k + 2))=    Underoverscript[∑ , k = 1, arg3] (1/(k + 1) - 1/(k + 2)) = Underscript[li ... , n∞] s_n = Underscript[lim , n∞] (1/2   - 1/(n + 2)) = 1/2

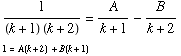
1/((k + 1) (k + 2)) = A/(k + 1) - B/(k + 2)  1 = A(k + 2) + B(k + 1)

Set k = -1, get A = 1;
Set k = -2, get B = -1;

Thus 1/((k + 1) (k + 2)) = 1/(k + 1) - 1/(k + 2)

s_n = (1/(1 + 1) - 1/(1 + 2)) + (1/(2 + 1) - 1/(2 + 2)) + (1/(3 + 1) - 1/(3 + 2)) + (1/(4 + 1) ... ;   +   1/5    - 1/6   + ... + 1/(n + 1) - 1/(n + 2)

   = 1/2   - 1/(n + 2)