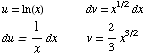Calculus II Quiz #5 March 26, 2004
Name____________________ R. Hammack Score ______
_________________________________________________________________
(1)
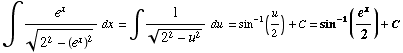
(2)
(3)
Now we use integration by parts a second time.
Now, the above expression says
From this we get
so
(4)