Calculus II Test #2 March 21, 2003
Name____________________ R. Hammack Score ______
_______________________________________________________________________________
(1) Find the area of the region contained between the graphs of
![[Graphics:HTMLFiles/test2_4.gif]](HTMLFiles/test2_4.gif)
To find where the graphs intersect, we solve the equation
x = 2
Thus the area is
(2) Consider the region contained between the y axis and the curve
Since y = y(1-y), the y intercepts are 0 and 1. Here is a picture.
![[Graphics:HTMLFiles/test2_13.gif]](HTMLFiles/test2_13.gif)
Using shells,
(3) Consider the region contained between the graphs of
This region is revolved around the x axis. Find the volume of the resulting solid
![[Graphics:HTMLFiles/test2_20.gif]](HTMLFiles/test2_20.gif)
Using slicing,
(4) Find the exact arc length of the curve
L =
(5) Consider the graph of
SA =
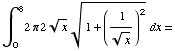
(6) A basement is 10 meters long, 10 meters wide, and 5 meters deep. After a heavy rain, the basement floods to a depth of 1 meter. Calculate the work required to pump all the water out to ground level. (Recall that the density of water is 1000 kilograms per cubic meter, and the acceleration due to gravity is 9.8 meters per second per second.)
Divide the water up into n layers each of thickness
Say the kth layer is at depth
The volume of each layer is (10)(10)
The density of each layer is (1000)(100)
The kth layer must be moved a distance of
The work done in moving this layer up it approximately
W = (force)(dist) = (mass)(accel)(dist) = (100000
Total work done in removing all layers is approximately
Total work done in removing all layers is exactly