Calculus II Test #1 March 5, 2003
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Find the following integrals.
(a)
(b)
(c)
(d)
(e)
(f)
(2) Find the following definite integrals.
(a)
(b)
(c)
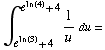
(d)
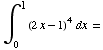
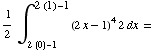
![1/2∫__ (-1)^1u^4du = 1/2[x^5/5] _0^1](HTMLFiles/test1_36.gif) =1/5
=1/5(3) The expression
![(Underoverscript[∑ , k = 1, arg3] x_k ^* cos(x_k ^*)^(1/2) Δx )](HTMLFiles/test1_40.gif) represents
a definite integral over the interval [3, 5]. Write the definite
integral. (You do not need to find its value.)
represents
a definite integral over the interval [3, 5]. Write the definite
integral. (You do not need to find its value.) (4) Find the average value of
(5) Find the following integrals. You may find it easiest to consider the area under the graphs.
(a)
Region is one fourth of a circle of radius 4.
(b)
Region is two triangles.
(6) Find the derivative of the function
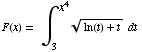
(7) A train, moving with constant acceleration, travels 25 miles in half an hour. At the beginning of the half-hour period, it has a velocity of 10 miles per hour. What is its velocity at the end of the half-hour period?
The information says:
s(0) = 0
s(1/2) = 25
v(0) = 10
Let a be the constant acceleration.
Know:
Then 1
Thus
If we could just find a, then we would have the formula for velocity, and the answer to the problem would be v(1/2). The information that we have not used yet is s(0) = 0 and s(1/2) = 25. That is information about position, so to use it we must make the position function.
Know:
Then
Thus
Now, 25 =
So 25 =
And 20 =
So a = 160
Finally, we now have the velocity function as
The velocity at the end of the half-hour period is v(1/2) = 160(1/2) + 10 = 90mph.
(8) Suppose that
(a)
(b)