Calculus II Test #1 March 5, 2003
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Find the following integrals.
(a)
(b)
(c)
(d)
(e)
(f)
_________________________________________________________________________________
Calculus II Test
#1 March
5, 2003
Name____________________ R. Hammack Score
______
_________________________________________________________________________________
(1) Find the following integrals.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) ![]()
(f) ![]()
(2) Find the following definite integrals.
(a) ![]()
(b) ![]()
(c) ![]()
(d) 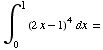
(3) The expression ![]()
![(Underoverscript[∑ , k = 1, arg3] x_k ^* cos(x_k ^*)^(1/2) Δx )](HTMLFiles/test1_40.gif) represents
a definite integral over the interval [3, 5]. Write the definite
integral. (You do not need to find its value.)
represents
a definite integral over the interval [3, 5]. Write the definite
integral. (You do not need to find its value.)
(4) Find the average value
of ![]() on the interval [0, 3].
on the interval [0, 3].
(5) Find the following integrals. You
may find it easiest to consider the area under the graphs.
(a) ![]()
(b) ![]()
(6) Find the derivative of the function
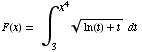
(7) A train,
moving with constant acceleration, travels 25 miles in half an hour. At
the beginning of the half-hour period, it has a velocity of 10 miles per hour. What
is its velocity at the end of the half-hour period?
(8) Suppose that ![]() and
and ![]() .
.
(a) ![]()
(b) ![]()