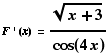Calculus II Quiz #3 February 26, 2003
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Use the Fundamental Theorem of Calculus to evaluate the following integrals. Simpify your answer as much as possible.
(a)
(b)
(c)
(2) Find the area of the region under the graph of
(3) Suppose
By F.T.C II,