____________________________________________________________
Calculus I Test #3 May 4, 2004
Name__________________ R. Hammack Score ______
____________________________________________________________
(1) Sketch the graph of the function 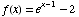 .
.
The function y = 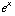 is drawn dashed.
is drawn dashed.
The function y = 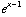 is the previous graph shifted one unit right. It's drawn dotted.
is the previous graph shifted one unit right. It's drawn dotted.
The function y = 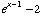 is the previous graph shifted 2 unit down. It's drawn solid.
is the previous graph shifted 2 unit down. It's drawn solid.
![[Graphics:HTMLFiles/T3S04C_6.gif]](HTMLFiles/T3S04C_6.gif)
(2) Find the inverse of the function 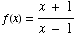 .
.
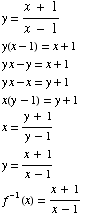
(3) Does the function 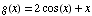 have an inverse? Explain.
have an inverse? Explain.
Notice that 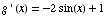 can have either positive or negative values, depending on x.
can have either positive or negative values, depending on x.
Examples:
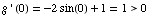
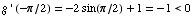
Thus the function g increases and decreases. It fails the Horizontal Line Test.
There is no inverse.
(4) Solve the equation 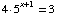 . (It's OK to have logarithms in your final answer.)
. (It's OK to have logarithms in your final answer.)
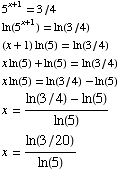
(5) Simplify the following expressions as much as possible.
(a) ![FormBox[RowBox[{RowBox[{(-32), ^, 0.2}], =}], TraditionalForm]](HTMLFiles/T3S04C_15.gif)
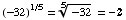
(b) 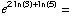
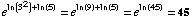
(c) 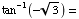
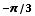
(d) 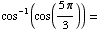
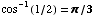
(6) Find the following derivatives.
(a) ![d/dx[ e^(x ln(x) )] =](HTMLFiles/T3S04C_23.gif)
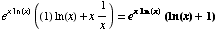
(b) ![d/dx[ ( ln ( tan^(-1)(x) ) )^3 ] =](HTMLFiles/T3S04C_25.gif)
![3 (ln ( tan^(-1)(x) ))^2d/dx[ ln ( tan^(-1)(x) ) ] = 3 (ln ( tan^(-1)(x) ))^21/(1 + x^2)/tan^(-1)(x) = (3 (ln ( tan^(-1)(x) ))^2)/(tan^(-1)(x) (1 + x^2))](HTMLFiles/T3S04C_26.gif)
(c) ![d/dx[ log_10(x) ] =](HTMLFiles/T3S04C_27.gif)
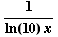
(d) ![d/dx[sin^(-1)(x^(1/2))] =](HTMLFiles/T3S04C_29.gif)
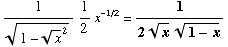
(7) The graph of the
derivative of a function f(x)
is drawn. Answer the following questions about the
function f(x).
![[Graphics:HTMLFiles/T3S04C_31.gif]](HTMLFiles/T3S04C_31.gif)
(a) Find the interval(s) on which f(x)
increases.
f(x) INCREASES
on ![(-∞, 0]](HTMLFiles/T3S04C_32.gif) and [2,3], because that's where its derivative is positive.
and [2,3], because that's where its derivative is positive.
(b) Find the critical points
of 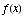 .
.
-3, 0, 2, 3
(c) Find the locations of
the relative extrema of 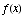 ,
and identify them as relative maxima or minima.
,
and identify them as relative maxima or minima.
Relative Max at 0 and 3 (Derivative
switches from + to -)
Relative Min at 2 (Derivative switches
from - to +)
(d) Find the intervals on
which the graph of f(x) is concave
up/down.
CONCAVE UP on [-3 ,-1] & [1, 2.5]
(That's where f ' increases,
so f " is positive.)
CONCAVE DOWN on ![(-∞ , -3]](HTMLFiles/T3S04C_35.gif) & [-1, 1] &
& [-1, 1] & ![FormBox[RowBox[{[, RowBox[{2.5, ,, ∞}], )}], TraditionalForm]](HTMLFiles/T3S04C_36.gif) (That's where f ' decreases,
so f " is negative.)
(That's where f ' decreases,
so f " is negative.)
(8) These problems are about
the function 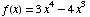 .
Answer the following questions about f(x).
.
Answer the following questions about f(x).
(a) Find the critical points of 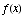 .
.
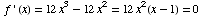
The critical points (which make the derivative 0) are 0
and 1
(b) Find the intervals of
increase/decrease of f(x).
0 1
----+---+-----
- - - - - | + + f '(x)
f increases on 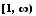
f decreases on ![(-∞, 1]](HTMLFiles/T3S04C_41.gif)
(c) Find the locations of
the relative extrema of 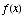 ,
and identify them as relative maxima or minima.
,
and identify them as relative maxima or minima.
Relative minimum at x = 1,
No relative maximum.
(d) Find the intervals on
which the graph is concave up/down.
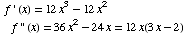
0 2/3
----+---+-----
+ +| - - | + + f ''(x)
f concave up on ![(-∞, 0],[2/3, ∞)](HTMLFiles/T3S04C_44.gif)
f concave down on ![[0, 2/3]](HTMLFiles/T3S04C_45.gif)
![[Graphics:HTMLFiles/T3S04C_6.gif]](HTMLFiles/T3S04C_6.gif)
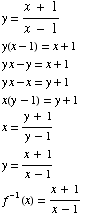
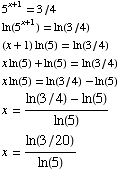
![[Graphics:HTMLFiles/T3S04C_31.gif]](HTMLFiles/T3S04C_31.gif)