____________________________________________________________________________
Calculus I                                                               Test #1                                      March  8, 2004

Name____________________                      R.  Hammack                                      Score ______
____________________________________________________________________________

(1)
(a)  cos(-(2π)/3) =

(b)  sec(-(2π)/3) =


(c) Find the domain of the function    f(x) = 1/(2^(1/2) sin(x) - 1).

 




(2)
(a) Sketch the graph of the equation    y = -1/3x - 2 .
[Graphics:HTMLFiles/test1sol_15.gif]

(b) Find the equation of the line that is parallel to the graph of   y = -1/3x - 2 (from Part a, above) and passes through the point (3, 4).  Put your final answer in slope-intercept form, and simplify as much as possible.

 


(3)   Suppose  f(x) = x/(x + 1) and   g(x) = 1/x .

(a)   f∘g(x) =

(b)   g∘f(x) =

(4) Sketch the graph of a function f(x) satisfying the following properties.
f(0) = 2,   f(2) = 1,    Underscript[lim , x2^-] f(x) = 3,   Underscript[lim , x2^+] f(x) = 1,   Underscript[lim , x -2] f(x) = ∞,    Underscript[lim , x∞] f(x) = ∞.  and   Underscript[lim , x -∞] f(x) = 0.

[Graphics:HTMLFiles/test1sol_36.gif]




(5)  The graph of a function f(x) is sketched. Use this information to find the following limits.
[Graphics:HTMLFiles/test1sol_39.gif]
(a)     Underscript[lim , x2] 4f(x) =

(b)     Underscript[lim , x -1] (f(x) + 2)/(f(x) + 3) =

(6)   Evaluate the following limits.

(a)    Underscript[lim , x -1] (2x^3 - 4x - 5) =

(b)  Underscript[lim , x2] (2x^2 - 8)/(x - 2) =

(c)    Underscript[lim , x2] (2x^2 - 8)/(x - 3) =

(d)   Underscript[lim , w25] (w - 25)/(w^(1/2) - 5) =

(e) Underscript[lim , x2] cos(π/(4 + x)) =

(f) Underscript[lim , x0] 1/(3x cot(x)) =


(7)  This problem concerns the function 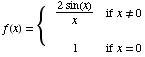f(x) = {   2sin(x) ------- x ... sp;x≠0 1 if  x = 0

(a) f(0) =

(b) Underscript[lim , x0] f(x) =

(c)  At which x values (if any) is the function f(x)  discontinuous? Explain  your answer.



(d)   Find the horizontal asymptotes (if any) of  f(x) .  Be sure to explain your work.