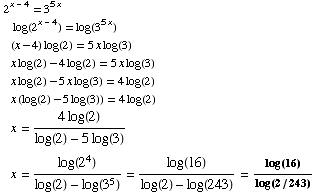Calculus I Quiz #9 April 20, 2004
Name____________________ R. Hammack Score ____
_____________________________________________________________
(1) Simplify the following expressions as much as possible.
(a)
(b)
(c)
(a)
(b)
(2) Write as a single logarithm:
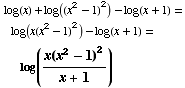
(3) Solve the equation: