___________________________________________________________
Calculus I                                            Quiz #8                       April 16, 2004

Name_________________             R.  Hammack                 Score ______
___________________________________________________________
(1) Find the inverse of the function f(x) = (2x - 1)^(1/3)

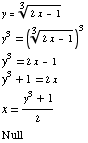
y = (2x - 1)^(1/3)  y^3 = ((2x - 1)^(1/3))^3  y^3 = 2x - 1  y^3 + 1 = 2x  x = (y^3 + 1)/2  Null
Now interchange x and y.
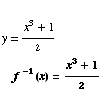
y = (x^3 + 1)/2f^( -1)(x) = (x^3 + 1)/2


(2)   Explain why the function  g(x) = x^5 + x^3 + x + 1 is invertible.

Note that the derivative g ' (x) = 5x^4 + 3x^2 + 1 is positive for all values of x.
Therefore the function g always increases, and never decreases.
Thus it passes the Horizontal Line Test, so it is invertible.



(3)  Consider the invertible function  g(x) = x^5 + x^3 + x + 1, from the previous question.
Find the value of x for which g^(-1)(x) = 1.

Notice that g(1) = 4, which means g^(-1)(g(1)) = g^(-1)(4), which is the same as 1 = g^(-1)(4).
Thus x = 4.


(4)  The graph of a one-to-one function is drawn. Draw the graph of its inverse.


We just reflect this graph across the line y=x, as illustrated.
[Graphics:HTMLFiles/quiz8sol_12.gif]