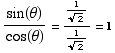Calculus I Quiz #4 February 24, 2004
Name____________________ R. Hammack Score ______
_______________________________________________________________________
(1)
(a)
(b)
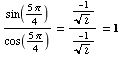
(c)
(2) Find the domain of the function
First, x can't be negative, for that would involve the square root of a negative number.
Second, x can't be such that 1+2cos(x) = 0, for that would result in division by zero.
The equation 1+2cos(x) = 0 reduces to cos(x) = -1/2,
so we are looking out for values of x that make cos(x) = -1/2.
Looking at the unit circle, you can see that
![[Graphics:HTMLFiles/quiz4_10.gif]](HTMLFiles/quiz4_10.gif)
Of course, you could add any multiple of
making the denominator in f(x) zero.
Conclusion: The domain is
(3) In this problem,
This information says
so it follows that
Then:
(a)
(b)