_____________________________________________________________________________________
Calculus I Test
#2 October
29, 2003
Name____________________ R. Hammack Score
______
_____________________________________________________________________________________
(1) Use the limit
definition of the derivative to find the derivative of the function 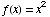 .
.
(2) The graph of a function 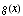 is a straight line that is inclined at an angle of 30 degrees, as illustrated
below. Find
is a straight line that is inclined at an angle of 30 degrees, as illustrated
below. Find 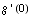 .
.
![[Graphics:HTMLFiles/T2F03Dsol_5.gif]](HTMLFiles/T2F03Dsol_5.gif)
(3) Sketch the graph of a function f for
which 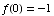 ,
,
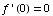 ,
, 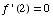 ,
,
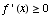 when
when 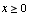 ,
and
,
and 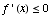 when
when 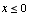 .
.
![[Graphics:HTMLFiles/T2F03Dsol_14.gif]](HTMLFiles/T2F03Dsol_14.gif)
(4) Suppose that the cost of drilling
x feet for an oil well is 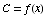 dollars, and suppose that
dollars, and suppose that 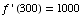 .
Explain, in non-mathematical terms, what the statement
.
Explain, in non-mathematical terms, what the statement 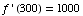 means.
means.
(5) ![d/dx[ 3x^4 + x + 2] =](HTMLFiles/T2F03Dsol_19.gif)
(6) ![d/dx[ -3/x^8 + 2x^(1/2)] =](HTMLFiles/T2F03Dsol_21.gif)
(7) ![d/ds[ 3/(2s + 1)] =](HTMLFiles/T2F03Dsol_23.gif)
(8) ![d/dx[ sec(x) tan(x) ] =](HTMLFiles/T2F03Dsol_25.gif)
(9) ![d/dx[sin(x) /x^2] =](HTMLFiles/T2F03Dsol_27.gif)
(10) If 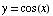 ,
find
,
find 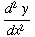 .
.
(11) ![d/dx[ (x^3 + 3x)^10] =](HTMLFiles/T2F03Dsol_33.gif)
(12) ![d/dx[ sin(x^3) ] =](HTMLFiles/T2F03Dsol_35.gif)
(13) ![d/dx[ sin(x^3)^(1/2)] =](HTMLFiles/T2F03Dsol_37.gif)
(14) ![d/dx[ x^5sec(1/x)] =](HTMLFiles/T2F03Dsol_39.gif)
(15) Suppose f is
a function for which 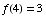 and
and 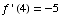 . If
. If
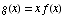 ,
find
,
find 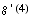 .
.
(16) Find all points on the
graph of 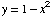 at
which the tangent line passes through the point (0, 2).
at
which the tangent line passes through the point (0, 2).
(17) Find the equation of
the tangent line to the graph of  at the point where
at the point where 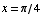 .
.
(18) A search light is trained
on a tall building. As the light rotates, the spot it illuminates moves up the
side of the building. That is, the distance D
between the ground and the illuminated spot is a function of the angle 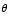 formed by the light beam and the horizontal ground. If the search light is located
50 meters from the building, find the function giving the rate of change of
D with respect to
formed by the light beam and the horizontal ground. If the search light is located
50 meters from the building, find the function giving the rate of change of
D with respect to 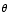 .
.
(19) Use implicit differentiation
to find 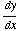 :
: 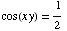 .
.
(20) A conical water tank
has a height of 24 feet and a radius of 12 feet, as illustrated. If water flows
into the tank at a constant rate of 20 cubic feet per minute, how fast is the
depth h of the water changing when
h = 2?
(Hint: You may be interested to know that the volume V
of a cone of height h and radius r
is 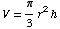 .)
.)
![[Graphics:HTMLFiles/T2F03Dsol_5.gif]](HTMLFiles/T2F03Dsol_5.gif)
![[Graphics:HTMLFiles/T2F03Dsol_14.gif]](HTMLFiles/T2F03Dsol_14.gif)