| Calculus I |
Quiz # 7
|
November 10, 2003
|
| Name____________________ |
Score ______
|
R. Hammack
|
(1) Find the inverse of the function
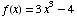 .
.
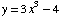
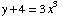
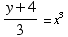
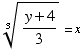
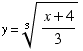
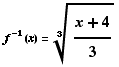
(2) Consider a one-to-one differentiable
function 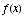 which satisfies the following table.
which satisfies the following table. 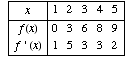
(a) 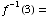
From the table, you see that 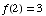 .
.
Thus, you get 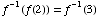 ,
,
and this is 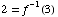 ,
,
Therefore 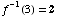
(b) If 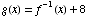 ,
find
,
find 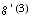 .
.
![g ' (x) = d/dx[f^(-1)(x) + 8] = d/dx[f^(-1)(x)] = 1/(f ' (f^(-1)(x)))](HTMLFiles/quiz7sol_17.gif)
Thus 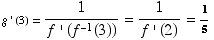
(3) Simplify the following
expressions as much as possible.
(a) 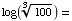

(b) ![FormBox[RowBox[{RowBox[{(-32), ^, RowBox[{(, RowBox[{-, 0.6}], )}]}], =}], TraditionalForm]](HTMLFiles/quiz7sol_21.gif)
![FormBox[RowBox[{StyleBox[RowBox[{1, /, RowBox[{(-32), ^, 0.6}]}], FontSize -> 16], =, 1/(-32)^(3/5) = 1/((-32)^(1/5))^3 = 1/(-2)^3 = -1/8}], TraditionalForm]](HTMLFiles/quiz7sol_22.gif)
(c) 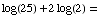
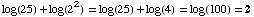
(d) 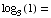 0
0
(e) 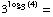 4
4
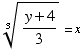
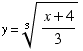
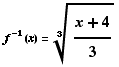

![FormBox[RowBox[{StyleBox[RowBox[{1, /, RowBox[{(-32), ^, 0.6}]}], FontSize -> 16], =, 1/(-32)^(3/5) = 1/((-32)^(1/5))^3 = 1/(-2)^3 = -1/8}], TraditionalForm]](HTMLFiles/quiz7sol_22.gif)