Calculus I Quiz #4 September 17, 2003
Name____________________ R. Hammack Score ______
__________________________________________________________________________
(1)
(a)
(b)
(c)
(d)
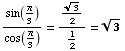
(e)
(2) Find all values of
From part d of the above problem, we see that one such value of
In general, you could add any multiple of
(3) Suppose
From
Now apply the identity
Then
(4) Consider the following triangle. Find
![[Graphics:HTMLFiles/quiz4sol_30.gif]](HTMLFiles/quiz4sol_30.gif)
By the Pythagorean Theorem, we have HYP =
Thus