Calculus I Quiz #3 September 10, 2003
Name____________________ R. Hammack Score ______
________________________________________________________________________
(1) Values for two functions
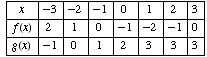
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h) Draw a rough sketch of the graph of
From the above work, we get the following table, from which the graph can be plotted.
![[Graphics:HTMLFiles/quiz3sol_20.gif]](HTMLFiles/quiz3sol_20.gif)
(2) The graph of a function
In red is sketched
![[Graphics:HTMLFiles/quiz3sol_26.gif]](HTMLFiles/quiz3sol_26.gif)
(3) Find the equation of the line that passes through the point (2,4) and is parallel to the line
Please put your answer in the slope-intercept form.
First the equation
So we are looking for a line of slope -3 and passing through the point (2,4). Using the point-solpe formula,