Calculus I 
Quiz  #2
September 5, 2003
Name____________________
R.  Hammack
Score ______

(1) Find the domain of the function f(x) = x/(x^2 - 2 x + 1)^(1/2)
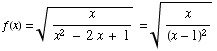
  f(x) = x/(x^2 - 2 x + 1)^(1/2) = x/(x - 1)^2^(1/2)

Notice that the denominator will be zero for x = 1.
Otherwise, the denominator is positive because it's squared.
So the only values of x that will make x/(x - 1)^2negative are negative values of x.
Conclusion: The domain is all nonnegative numbers except 1.
i.e. Domain is [0, 1)and (1, ∞).


(2) Consider the function g(x) = { 1 -              ... 2 x              if x <= 3
(a)   g(-2) =2 (-4) = -4
(b)   g(π) =1/π
(c)   g ( h^2 + 4) =1/(h^2 + 4) (because no matter the value of h, h^2 + 4 > 3.



(3) Consider the function f(x) = x^2 - 6 x + 8.

(a)    For what value(s) of x is f(x) = 3?
Solve x^2 - 6 x + 8 = 3
  x^2 - 6 x + 5 = 0
  (x - 1) (x - 5) = 0

x  = 1  or x = 5

(c)     For what value(s) of x is f(x) < 0?

f(x) = x^2 - 6 x + 8 = (x - 4) (x - 2)

       2    4
----+---+--------
- - - - - - + + +(x-4)
- - - + + + + +(x-2)
+ + - - - + + +f(x) = (x-4)(x-2)

f(x) will be negative for all values of x between 2 and 4.