Calculus I Test #1 October 5, 2004
Name _________________ R. Hammack Score______
Directions. Answer in the space provided. Show as much work as is reasonable.
_______________________________________________________________
(1)
(a)
(b)
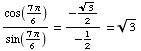
(c) Suppose
Suppose for the moment that the problem were
Since
![[Graphics:HTMLFiles/index_10.gif]](HTMLFiles/index_10.gif)
Then
However, in this problem
(d) Find all solutions of the equation
![[Graphics:HTMLFiles/index_15.gif]](HTMLFiles/index_15.gif)
From the unit circle, you can see that the solutions are
(2) Suppose
(a)
(b)
(c)
(d)
(e) State the domain of g.
(f) State the range of g.
(3) A line has slope 9 and passes through the point (20, 4). What is its x-intercept?
By the point-slope formula, the equation of the line is
Now, to find the x-intercept, set y = 0, and solve for x.
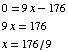
(4)
(5)
(6)
(7)
![Underscript[lim , x -2] (2 + x)/(2x) /(x + 2) = Underscript[lim , x -2] (2 + x ... x -2] (2 + x)/(2x) 1/(2 + x) = Underscript[lim , x -2] 1/(2x) = 1/(2 (-2)) = -1/4](HTMLFiles/index_38.gif)
(8)
(9)
![Underscript[lim , x∞] (2 + 1/x)/((3x^2 + 1) (1/x)^2)^(1/2) = Underscript[lim , x∞] (2 + 1/x)/(3 + 1/x^2)^(1/2) = (2 + 0)/(3 + 0)^(1/2) = 2 /3^(1/2)](HTMLFiles/index_43.gif)
(10)
(11)
(12)
(13)
(14) Consider the function
Note
(a) At which values of x is f discontinuous?
0 and -3 because f is not defined there
(b) Find the vertical asymptotes (if any) of f.
The denominator is 0 for x = 0 or -3. These are the candidates for the locations of the vertical asymptotes.
(c) Find the horizontal asymptotes (if any) of f.
(d) For which values of x does
We need to solve
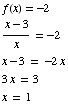
Answer: x = 1