Calculus I Quiz #8 November 9, 2004
Name____________________ R. Hammack Score ______
_______________________________________________________________________
(1) Suppose an invertible function f and its derivative obey the following table.
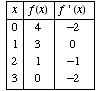
(a)
(b) Is
(c) If
Using the formula for the derivative of an inverse, we get:
Thus:
(2) Find the inverse of the function
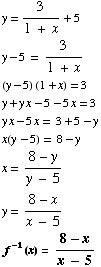
(3) The graph of a function f is drawn. Sketch the graph of its inverse.
The graph is obtained by reflecting the given graph across the line y = x.
![[Graphics:HTMLFiles/Q8F04A_11.gif]](HTMLFiles/Q8F04A_11.gif)