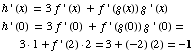Calculus I Quiz #7 October 28, 2004
Name____________________ R. Hammack Score ______
_______________________________________________________________________
(1) Find derivatives of the following functions.
(a)
(b)
(c)
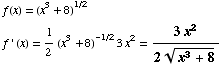
(2) Suppose functions f and g and their derivatives obey the following table.
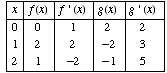
If