Calculus I Quiz #6 October 22, 2004
Name____________________ R. Hammack Score ______
_______________________________________________________________________
(1) Find derivatives of the following functions.
(a)
(b)
(c)
(2) If
(3) Suppose functions f and g and their derivatives obey the following table.
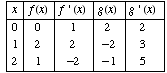
If
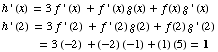
(3) Find the values of x at which the slope of the tangent to the graph of
Finding the values of x for which the tangent line is horizontal (slope 0) amounts to solving
Answer: x = 0 and x = 1