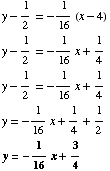_______________________________________________________________________
Calculus I                                                          Quiz #5                            October 15, 2004

Name____________________                   R.  Hammack                              Score ______
_______________________________________________________________________

(1) Use the limit definition of the derivative to find the derivative of the function  f(x) = 1/x^(1/2).
  f ' (x) = Underscript[lim , wx] (f(w) - f(x))/(w - x) = Underscript[lim , wx] ... 1/2))/(w - x) = Underscript[lim , wx] (x^(1/2) - w^(1/2))/(w^(1/2) ( x)^(1/2))/(w - x)/1 =
  
  Underscript[lim , wx] (x^(1/2) - w^(1/2))/(w^(1/2) ( x)^(1/2)) 1/(w - x) = Underscript ... (w^(1/2) + x^(1/2))) = Underscript[lim , wx] -1/((w^(1/2) ( x)^(1/2)) (w^(1/2) + x^(1/2)))

-1/((x^(1/2) ( x)^(1/2)) (x^(1/2) + x^(1/2))) = -1/(x^(1/2) ( x)^(1/2) 2x^(1/2) ) = -1/(2x^(1/2)^3 )




(2)  Use your answer from Question 1 to find the slope of the tangent line to the graph of the function f(x) = 1/x^(1/2)
at the point where x = 4. (You do not need to use a limit to answer this question.)


slope =  f ' (4) = -1/(24^(1/2)^3 ) = -1/16



(3)   Use your answer from Question 2 to find the equation of the tangent line to the graph of the function f(x) = 1/x^(1/2)
at the point where x = 4. Please put your final answer in slope-intercept form.

From above, the slope if 1/16.   A point on the tangent line is (4, f(4)) = (4, 1/2). Equation of line is thus:

y - 1/2 = -1/16 (x - 4)  y - 1/2 = -1/16x + 1/4  y - 1/2 = -1/16x + 1/4  y = -1/16x + 1/4 + 1/2  y = -1/16x + 3/4