Calculus I Quiz 3 September 21, 2004
Name _________________ R. Hammack Score_____
_____________________________________________________________
(1) Find the equation of the line that passes through the point (5, 9) and has x-intercept 7.
Please express your answer in slope-intercept form.
We know 2 points on the line. (5, 9) and (7, 0). Thus its slope is
Using the point-slope form of the equation for a line, we get
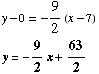
(2)
(a)
![[Graphics:HTMLFiles/Q3F04A_5.gif]](HTMLFiles/Q3F04A_5.gif)
(b)
(Because any radian measure that's an odd multiple of
(3) Find all values of x (in radians) for which
From the unit circle, you can see that if
![[Graphics:HTMLFiles/Q3F04A_10.gif]](HTMLFiles/Q3F04A_10.gif)
But note also you can add any integer multiple of
SOLUTION:
(4) Suppose x is a number for which
From the identity
Thus
Now,