Calculus I Quiz #10 November 23, 2004
Name____________________ R. Hammack Score ______
_______________________________________________________________________
(1)
(a)
(b)
![[Graphics:HTMLFiles/Q10F04A_5.gif]](HTMLFiles/Q10F04A_5.gif)
(c) Sketch the graph of
![[Graphics:HTMLFiles/Q10F04A_7.gif]](HTMLFiles/Q10F04A_7.gif)
(2)
(a) f '(x) =
(b)
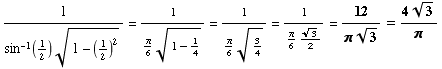
(3)
(a) f '(x) =
(b)
_______________________________________________________________________
Calculus I Quiz
#10 November
23, 2004
Name____________________ R. Hammack Score
______
_______________________________________________________________________
(1)
(a) ![]()
![]()
(b) ![]()
![]()
![[Graphics:HTMLFiles/Q10F04A_5.gif]](HTMLFiles/Q10F04A_5.gif)
(c) Sketch the graph of
![]() . Please
indicate any asymptotes.
. Please
indicate any asymptotes.
![[Graphics:HTMLFiles/Q10F04A_7.gif]](HTMLFiles/Q10F04A_7.gif)
(2) ![]()
(a) f
'(x) = ![]()
(b) ![]()
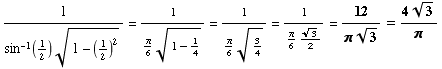
(3) ![]()
(a) f
'(x) = ![]()
(b) ![]()
![]()