__________________________________________________________________________________
Calculus I Final
Exam December
10, 2002
Name____________________ R. Hammack Score
______
_________________________________________________________________________________
(1) Evaluate the following limits.
(a) ![Underscript[lim , x3] (x^2 - 2x )/(x + 1) =](HTMLFiles/ExF02_1.gif)
(b) ![Underscript[lim , x4] (x^2 - 16)/(x - 4) =](HTMLFiles/ExF02_3.gif)
(c) ![Underscript[lim , x4] (4 - x)/(2 - x^(1/2)) =](HTMLFiles/ExF02_5.gif)
(d) ![Underscript[lim , xπ^+] cot(x) =](HTMLFiles/ExF02_7.gif)
(e) ![Underscript[lim , x∞] (6x^5 + x)/(3x^5 - 8) =](HTMLFiles/ExF02_9.gif)
(f) ![Underscript[lim , x2] sin(2x - 4)/(x^2 - 4) =](HTMLFiles/ExF02_11.gif)
(2) Use the limit
definition of the derivative to find the derivative of the function 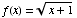 .
.
(3) Find the following derivatives.
(a) ![d/dx[ 3x^8 + 2x + 1 ] =](HTMLFiles/ExF02_16.gif)
(b) ![d/dx[ sin(π) + ln(x) ] =](HTMLFiles/ExF02_18.gif)
(c) ![d/dx[ x^(1/2) + 1/x ] =](HTMLFiles/ExF02_19.gif)
(d) ![d/dx[ (2x - 1)/(x + 3) ] =](HTMLFiles/ExF02_21.gif)
(e) ![d/dx[ (x sin(x))/(x + 1) ] =](HTMLFiles/ExF02_23.gif)
(f) ![d/dx[ x e^x] =](HTMLFiles/ExF02_25.gif)
(g) ![d/dx[ cos(5x)^(1/2) ] =](HTMLFiles/ExF02_27.gif)
(h) ![d/dx[ x^3sec(1/x) ] =](HTMLFiles/ExF02_29.gif)
(i) ![d/dx[ ln(1 - x e^(-x)) ] =](HTMLFiles/ExF02_32.gif)
(j) ![d/dx[ x^x ] =](HTMLFiles/ExF02_34.gif)
(k) ![d/dx[ e^( sin^(-1)(x)) ] =](HTMLFiles/ExF02_43.gif)
(4) Simplify the following expressions
as much as possible.
(a) 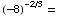
(b) 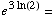
(c) ![FormBox[RowBox[{RowBox[{log_10, (, 0.001, )}], =}], TraditionalForm]](HTMLFiles/ExF02_49.gif)
(d) 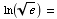
(e) 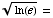
(f) 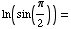
(g) 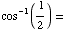
(h) 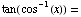
(i) 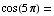
(j) 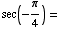
(5) Sketch the graph
of 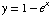
![[Graphics:HTMLFiles/ExF02_68.gif]](HTMLFiles/ExF02_68.gif)
(6) Solve the equation 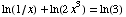 for
x.
for
x.
(7) The questions on this page concern
the one-to-one function 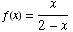
(a) ![Underscript[lim , x2^+] f(x) =](HTMLFiles/ExF02_77.gif)
(b) ![Underscript[lim , x∞] f(x) =](HTMLFiles/ExF02_79.gif)
(c) List the vertical asymptotes
of f (if any).
(d) List the
horizontal asymptotes of f (if
any).
(e) Find the inverse of
f.
(f) State the domain of f. All
values of x except 2.
(g) State the domain of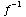 .
.
(h) State the range of f.
(i) State the range
of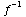 .
.
(j) Find the equation of the tangent
line to the graph of 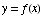 at
the point where
at
the point where 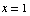 .
.
(8) This problem concerns the function
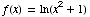 .
.
(a) 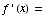
(b) 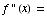
(c) Find the interval(s)
on which f is
increasing and on which it is decreasing.
(d) Find the interval(s)
on which f is
concave up and on which it is concave down.
(e) List the x-coordinates
of all inflection points of f.
(f) List all the critical
numbers of f.
(g) List the x-coordinates
of the relative extrema of f (if
any) and say whether there is a relative minima or a relative maxima.
(9) Given the equation 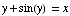 , find
, find 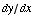 .
.
(10) A rectangular box with with two
square sides and an open top is to have a volume of 36 cubic feet. Find the
dimensions of the container with minimum surface area.
![[Graphics:HTMLFiles/ExF02_118.gif]](HTMLFiles/ExF02_118.gif)
(11) A spherical balloon is deflated
in such a way that its radius decreases at a constant rate of 15 cm/min. At
what rate is air escaping when the radius is 2 cm?
Hint: The volume of a sphere of radius r is 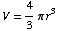 .
.
![[Graphics:HTMLFiles/ExF02_68.gif]](HTMLFiles/ExF02_68.gif)
![[Graphics:HTMLFiles/ExF02_118.gif]](HTMLFiles/ExF02_118.gif)