_____________________________________________________________________________
Calculus  I                                                     Final Exam                                    December 13, 2001

Name____________________                R.  Hammack                                            Score ______
_____________________________________________________________________________
(1) Calculate the limits.
  
(a)    Underscript[lim , x3]    2x^2 + x - 1 = 2 (3^2) + 3 - 1 = 20

(b)    Underscript[lim , x0]   ((1 + x )^(1/2) - 1)/x =   Underscript[lim , x0]   ((1 + x )^(1/2) - 1)/x ((1 + x )^(1/2) + 1)/((1 + x )^(1/2) + 1) =  Underscript[lim , x0]   (1 + x - 1)/x ((1 + x )^(1/2) + 1) =
  Underscript[lim , x0]   1/((1 + x )^(1/2) + 1) =  1/((1 + 0 )^(1/2) + 1) = 1/2

(c)     Underscript[lim , x4]   (16 - x^2)/(x - 4) =    Underscript[lim , x4]   ((4 - x) (4 + x))/(x - 4) =  Underscript[lim , x4]   -(4 + x) = -8

(2) Find the derivatives of the following functions. You may use any applicable rule. You do not need to simplify your answer.
  
(a)    f(x) = 3x^4 + 2x   - ln(x) + e^x      f ' (x) = 12x^3 + 2 - 1/x + e^x

(b)   f(x) = (2 + x^6)/(cos x)     f ' (x) = (6x^5cos(x) + ( 2 + x^6) sin(x))/(cos x)^2



(c)  y = sin ( tan(x) )   dy/dx = cos(tan(x)) sec^2(x)


(d) d/dx[ tan^(-1)(2 + ln x) ] =(1/x)/(1 + (2 + ln(x))^2) =1/x(1 + (2 + ln(x))^2)

(e) d/dx[x^2e^sec (x)] = 2x e^sec (x) + x^2e^sec (x) sec(x) tan(x)


(3) The questions on this page concern the function f(x) = 1/(x - 3)^(1/3)

(a)    Underscript[lim , x4] f(x) = 1/(4 - 3)^(1/3) = 1

(b) Underscript[lim , x∞] f(x) = 0

(c)  Underscript[lim , x3^+]   f(x)    =   infinity

(d) State the horizontal asymptotes of f.    Line y = 0

(e) State the vertical asymptotes of f.   Line x = 3

(f) Find the inverse of f.  (You may assume that f is one-to-one.)

y = 1/(x - 3)^(1/3)

x = 1/(y - 3)^(1/3)

x^3 = 1/(y - 3)

x^3(y - 3) = 1

x^3y - 3x^3 = 1

x^3y = 1 + 3x^3

y = (1 + 3x^3)/x^3

f^( -1)(x) = (1 + 3x^3)/x^3

(g) Find the derivative of f.
  f(x) = 1/(x - 3)^(1/3) = (1/(x - 3))^(1/3) = (x - 3)^(-1/3)

f ' (x) = - 1/3 (x - 3)^(-4/3) (1) =-1/(3 (x - 3)^(1/3)^4)


(h) Find the equation of the line tangent to the graph of  y = f(x) at the point x = 2.
  
  Point: (2, f(2)) = (2, 1/(2 - 3)^(1/3)) = (2, -1)
  Slope: f ' (2) = -1/(3 (2 - 3)^(1/3)^4) = -1/3
  
  By Point-Slope Formula:
  y - (-1) = -1/3 (x - 2)
  y + 1 = -1/3 x + 2/3
  y = -1/3  x - 1/3

(4) This problem concerns the function  f(x) = x^2 + 2x  .

(a)  f ' (x) = 2x + 2

(b) Find all critical points of f.
x = -1

(c) Find the absolute maximum and minimum values of f on the interval [-2, 2].
f(-2) = (-2)^2 + 2 (-2) = 0   
f(2) = (2)^2 + 2 (2) = 8
f(-1) = (-1)^2 + 2 (-1) = -1

Absolute Maximum is 8, which happens at x = 2.
Absolute Minimum is -1, which happens at x = -1.


(5) This problem concerns the function f(x) = ln (   (x^2 - 1)^2 + 1 ) .

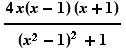
(a)  f ' (x) =   (2 (x^2 - 1) 2x)/((x^2 - 1)^2 + 1) = (4x(x - 1) (x + 1))/((x^2 - 1)^2 + 1)


(b) Find all critical points of f.
-1, 0, 1

(c) State the intervals on which f is increasing and those on which it is decreasing.
      -1      0      1
----+-----+----+-----
- - -| + + | - - -| + + + f  '(x)

Increases on (-1, 0) and (1, ∞)
Decreases on (-∞, -1) and (0, 1)

(d) List the locations of all relative maxima of f.   x = 0

(e) List the locations of all relative minima of f.   x = -1, x = 1.
(6)  Use the limit definition of the derivative to find the derivative of f(x) = 1/x.

Underscript[lim , wx] (f(w) - f(x))/(w - x) =Underscript[lim , wx] (1/w - 1/x)/(w - x) =Underscript[lim , wx] (x - w)/(w x)/(w - x) =Underscript[lim , wx] -1/(w x) =-1/x^2


(7) Find all values of x for which the slope of the tangent line to the graph of  y = cot(x)  at  x has slope FormBox[RowBox[{-, 4.}], TraditionalForm]

slope = dy/dx = -csc^2(x) = -4
csc^2(x) = 4
csc(x) = ± 2
1/sin(x) = ± 2
sin(x) = ± 1/2

x = ± π/6 + n π, where n is an integer.


(8) Consider the equation e^(x - y) = y .

(a) Find dy/dx.

d/dx[e^(x - y)] = d/dx[y]

e^(x - y)(1 - dy/dx) = dx/dx

e^(x - y) - e^(x - y) dy/dx = dx/dx

e^(x - y) = dx/dx + e^(x - y) dy/dx

e^(x - y) = (1 + e^(x - y)) dy/dx

dy/dx = e^(x - y)/(1 + e^(x - y))



(b) Find the slope of the tangent line to the graph of   e^(x - y) = y   at the point  (1, 1).

Plugging this point into the above expression gives dy/dx = e^(1 - 1)/(1 + e^(1 - 1)) = 1/2


(9) Suppose you have 600 feet of fencing material to enclose two rectangular regions, as illustrated. What dimensions x and y would enclose the greatest area?
------------------
|         |           |
|         |           |
|         |           |
-----------------

Call the horizontal length x and the vertical length y
Then 2x + 3y = 600,   so y = (600 - 2x) / 3

We want to maximize area = x y = x(600 - 2x) / 3 = (600x - 2x^2) / 3 on the interval [0, 300].
Let A(x) = (600x - 2x^2) / 3
So A ' (x) = (600 - 4x) / 3  = 0
The critical number is then x = 150.
Since A ''(x) = -4 < 0, the second derivative test says this must be a relative maximum,
and since there's only one critical number, this must be an absolute maximum.

Therefore, area is maximized when x = 150 feet and y = 100.
Thus the fenced area should be 150 by 100 feet.


(10) The height of a conical bucket is 3 feet and its radius is 1 foot. Water is poured into the bucket at a rate of 1 cubic foot per minute. How quickly is the depth h of the water increasing when h  = 2?

Let V be the volume of the water in the bucket.
We know: dV / dt = 1
We want: dh / dt

Formula for the volume of a cone of radius r and height h is V = 1/3π r^2h .
By similar triangles, r = h/3, thus
V = 1/3π (h/3)^2h

V = π/27 h^3

d/(d t)[V] = d/(d t)[π/27 h^3]

dV/dt =π/9h^2dh/dt

1 =π/92^2dh/dt


dh/dt = 9/(4π)feet per minute
(11)  An object, moving on a horizontal line, is a distance of   s(t) = t ^3 - 6t^2 + 9t + 1  feet from a point A at time t . (t is in seconds.)

(a) At what time(s) t is the object a distance of 1 foot from the point A?
When  1 = s(t)
1 = t ^3 - 6t^2 + 9t + 1
0 = t ^3 - 6t^2 + 9t
0 = t(t ^2 - 6t + 9)
0 = t(t - 3) (t - 3)
ANSWER: At times t = 0 and t = 3

(b) Find the function giving the object's velocity at time t.
  v(t) = s ' (t) = 3t ^2 - 12t + 9

(c) Find the function giving the object's acceleration at time t.
  a(t) = v ' (t) = 6t - 12

(d) At what time(s)  t does the object have a velocity of 9 feet per second?
When  9 = v(t)
  9 = 3t ^2 - 12t + 9
  0 = 3t ^2 - 12t
  0 = 3t(t - 4)
ANSWER: At times t = 0 and t = 4

(e) At what time(s)  t does the object change direction?
This will happen when the velocity  v(t) = 3t ^2 - 12t + 9 changes sign.
v(t) = 3t ^2 - 12t + 9 = 3 (t ^2 - 4t + 3) = 3 (t - 1) (t - 3)
       1     3
-----+----+-----
+ + | - - -| + + v(t)
ANSWER: Object changes direction at times t = 0 and t = 4

(f) When is the object's acceleration 0 feet per second per second?
When  0 = a(t)
  0 = 6t - 12
  t = 2
ANSWER: At time t = 2

(g) Find the times at which the object is speeding up.
This will happen when velocity and acceleration have the same sign.
Here is a chart for the sign of acceleration.

     2
---+-------
- - | + + + a(t) = 6t - 12

From this chart and the one for velocity in part e, we see that the object is speeding up on the time intervals [1,2] and [3, ∞]

(h) When does the object attain its minimum velocity? (Remember, that velocity could be negative.)
To find the minimum of v(t), we must look at the critical numbers of v(t).
Since v ' (t) = a(t) = 6t - 12, the only critical number is t = 2.
The chart from part g shows that there is a relative minimum there, so that must be an absolute minimum (since there is just one critical number).
ANSWER: At time t = 2