(1) Suppose f(x) =
f '(x) =
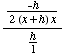
=
(2) Find the derivatives of the following functions. You may use any applicable rule.
(a) f(x) = 4
f '(x) = 40
(b) f(x) =
f ' (x) =
(c) y = x tan(x)
dy/dx = (1)tan x + x
(d)
(e)
(3) Suppose f(x) equals the number of dollars it costs to erect an x-foot-high transmitting tower.
(a) What are the units of f '(x)?
dy/dx = dollars per foot
(b) Suppose that f '(100) = 105. Explain, in ordinary English, what this means.
It will cost $105 to build the 101st foot
(4) This problem concerns the function f that is graphed below
![[Graphics:HTMLFiles/2F01sol_39.gif]](HTMLFiles/2F01sol_39.gif)
(a) Sketch the graph of f '(x). (Use the same coordinate axis)
(b) Suppose g(x) = sin(f(x)). Find g '(4).
By the chain rule, g '(x) = cos( f(x) ) f '(x),
so g '(4) = cos(f(4)) f '(4) = cos(1)(0) = 0
(c) Suppose h(x) = 4 +
h '(x) = 2x + 2x f(x) +
so h '(2) = 2(2) + 2(2)(f(2)) +
(5) Sketch the graph of a function f whose derivative has the following properties:
f(0) = 2, f '(0) = 0, f '(3) = 0, and f '(x) ≤ 0 for all values of x.
![[Graphics:HTMLFiles/2F01sol_45.gif]](HTMLFiles/2F01sol_45.gif)
(6) Consider the function f(x) = x +
(a) Find the slope of the tangent line to the graph of f at the point where x = 4.
f '(x) = 1 +
(b) Find the equation of the tangent line to the graph of f at the point where x = 4.
The slope is 5/4 (from part a), and the line passes through the point (4, f(4)) = (4, 6).
Using the point-slope formula:
y - 6 = 5/4(x - 4)
y - 6 = 5/4 x - 5
y = 5/4 x + 1
(7) Find all values of x for which the slope of the tangent to the graph of y = sin x at the point x is
Slope = dy/dx = cos x, so we are looking for all values of x for which cos x = 1/2.
Looking at the unit circle, we see that these values of x are x = π/3 + k2π and x = -π/3 + k2π , where k is an integer.
(8) Find the slope of the tangent to the graph of
(9) Suppose a 10-foot-long ladder is sliding down a wall in such a way that the base of the ladder moves away from the wall at a constant rate of 2 feet per second. How fast is the top of the ladder moving down the wall when it is 6 feet above the floor?
Let x be the distance from the wall to the base of the ladder. Let y be the height of the top of the ladder.
We know
By the Pythagorean Theorem,
2x
Now use the Pythagorean Theorem again to find that x = 8 when y = 6.
Then