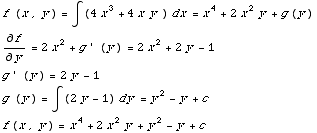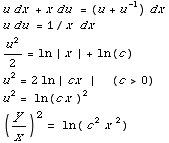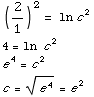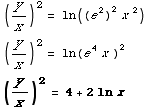______________________________________________________________________
Differential Equations Test #1 March 4, 2005
Name____________________ R. Hammack Score ______
______________________________________________________________________
(1) Which of the following (if any) is a solution to the differential equation 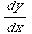 =-
=-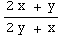 .
.
(a) 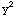 + x y +
+ x y +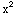 =2
=2
Differentiating implicitly gives 2y y'+y+x y' +2x =0.
Solving for y ' gives
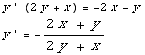
THIS IS A SOLUTION
(b) 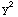 + 2x y +
+ 2x y +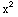 =1
=1
Differentiating implicitly gives 2y y'+2y+2x y' +2x =0.
Solving for y ' gives
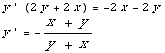
THIS IS NOT A SOLUTION
(2) Consider the differential equation (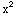 -y)y'=y+x. Describe the region of the xy-plane for which this differential equation would have a unique solution through any point (
-y)y'=y+x. Describe the region of the xy-plane for which this differential equation would have a unique solution through any point (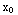 ,
, 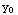 ) in the region. Please explain your conclusion.
) in the region. Please explain your conclusion.
Here we have y'=f(x,y)=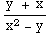 and
and 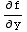 =
=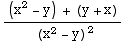 . Both of these functions are continuous except where their denominators are zero. Their denominaors are zero at (
. Both of these functions are continuous except where their denominators are zero. Their denominaors are zero at (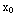 ,
, 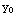 ) exactly when
) exactly when 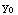 =
= 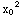 . Thus Theoreom 1.1 asserts there is a unique solution through any point (
. Thus Theoreom 1.1 asserts there is a unique solution through any point (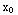 ,
, 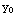 ) that is not on the parabola y=
) that is not on the parabola y=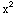 . The region is thus entire plane minus the points on the prabola.
. The region is thus entire plane minus the points on the prabola.
(3) Solve: (1+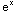 )
)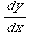 +
+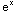 =0
=0
The variables can be separated.
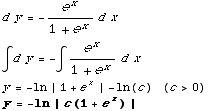
(4) Solve: cos(x)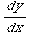 +y sin(x)=1
+y sin(x)=1
Notice that this is a linear D.E. Let's begin by putting it in standard form. Divide both sides by cos(x).
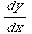 +tan(x)y =sec(x)
+tan(x)y =sec(x)
The integrating factor is 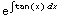 =
=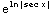 =|sec x|
=|sec x|
It doesn't matter whether we multiply both sides by positive or negative sec x (we're still multiplying both sides by the same expression), so let's multiply both sides by sec x.
![sec(x) dy/dx + sec(x) tan(x) y = sec^2 (x) d/dx[sec (x) y] = sec^2 (x) sec (x) y = ∫sec^2(x) dx sec (x) y = tan (x) + c y = sin(x) + c cos(x)](HTMLFiles/T1S05C_30.gif)
(5) Solve: (1-2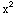 -2y)
-2y)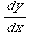 =4
=4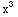 +4x y
+4x y
(4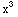 +4x y)dx+(2
+4x y)dx+(2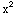 +2y-1)dy=0
+2y-1)dy=0
Note that 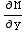 =4x=
=4x=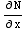 so the D.E. is exact.
so the D.E. is exact.
This means there is some function f(x,y) for which 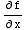 =4
=4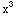 +4x y
+4x y
and 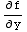 =2
=2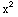 +2y-1, and f(x,y)=c will be a general solution to the D.E.
+2y-1, and f(x,y)=c will be a general solution to the D.E.
Now we find f.
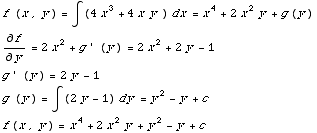
SOLUTION TO D.E. is 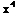 +2
+2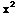 y+
y+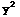 -y=c
-y=c
(6) This problem concerns the differential equation 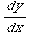 =
=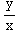 +
+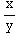
(a) Find a general solution.
dy=(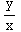 +
+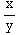 )dx
)dx
Note this is homogeneous of degree 0. Set y=ux, dy = u dx + x du.
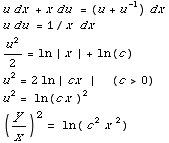
(b) Find the specific solution subject to the initial condition y(1)=2.
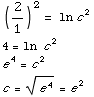
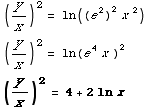
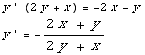
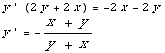
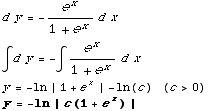
![sec(x) dy/dx + sec(x) tan(x) y = sec^2 (x) d/dx[sec (x) y] = sec^2 (x) sec (x) y = ∫sec^2(x) dx sec (x) y = tan (x) + c y = sin(x) + c cos(x)](HTMLFiles/T1S05C_30.gif)