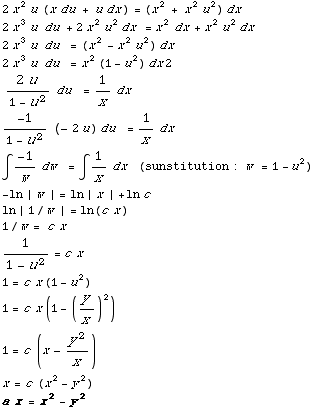Differential Equations Quiz #3 March 11, 2005
Name____________________ R. Hammack Score ______
_________________________________________________________________________________
(1) Find the orthogonal trajectory of
Differentiating implicitly with respect to x gives
3
from which we get y'=-
Thus, the orthogonal trajectory must have D.E.
This is a homogeneous differential equation.
We use the substitution y = ux, dy = x du +u dx.