_________________________________________________________________________________
Differential Equations                                        Quiz #2                                             February 25, 2005

Name____________________                   R.  Hammack                                                 Score ______
_________________________________________________________________________________

(1)     Solve the differential equation  dy/dx=(x^2y^2)/(1 + x)

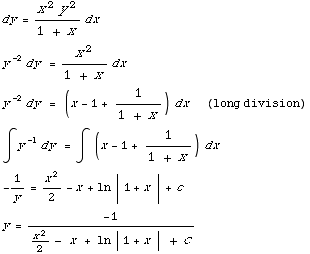
dy = (x^2y^2)/(1 + x) dx  y^(-2) dy = x^2/(1 + x) dx  y^(-2) dy = (x - 1 + 1 ... ) dx  -1/y = x^2/2 - x + ln | 1 + x | + c  y = -1/(x^2/2 - x + ln | 1 + x | + c)


(2)  Solve the differential equation  2x^2dy/dx=3x y+y^2  subject to the initial condition y(1)=-2.

This becomes  2x^2dy=(3x y+y^2)dx which is a homogeneous D.E.
Use substitution u=y/x;    y = ux;   dy=u dx +x du, and this becomes
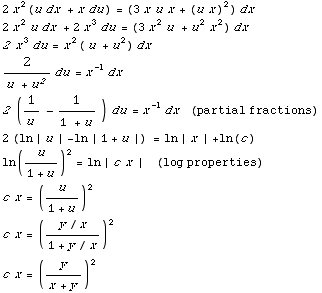
2x^2 (u dx + x du) = (3x u x + (u x)^2) dx  2x^2u dx + 2x^3 du = (3x^2 u + u^2 x^2) ... es)  c x = (u/(1 + u))^2  c x = ((y/x)/(1 + y/x))^2  c x = (y/(x + y))^2
Now plug in (x,y)=(1,-2) and get
c =(-2/(1 - 2))^2=4
SOLUTION:  4 x=(y/(x + y))^2

(3)  It the solution to the initial value problem in the previous question (2) unique?  Why or why not.
That D.E. is   dy/dx=f(x,y)=(3x y + y^2)/(   2x^2).

Both  f and ∂f/∂y=(3x + 2y)/(   2x^2) are continuous at (1, -2), so Theoreom 1.1 asserts the solution is unique.