_________________________________________________________________________________
Differential Equations                                        Quiz #1                                             February 14, 2005

Name____________________                   R.  Hammack                                                 Score ______
_________________________________________________________________________________
(1)     The first column in the table contains three differential equations. For each equation, determine whether it's linear, and what its order is.

Differential Equation Linear? (Yes/No) Order
x^2y + cos(y) y ' - sin(x) y'' = e^x NO 2
y - x = 3dy/dx + x (d^2y)/(d x^2) + x^(1/2) (d^3y)/(d x^3) YES 3
x^2 (d^2y)/(d x^2) + x^(1/2) dy/dx (d^3y)/(d x^3) = 5x NO 3


(2)  Consider the differential equation (d^2y)/dx^2-2/x^2y=0
For parts (a), (b), (c) and (d) decide if the given function is a solution.
Please show your work.

(a)   y=x^2
y'' = 2
Plugging this information into the equation gives
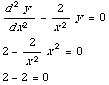
(d^2y)/dx^2 - 2/x^2y = 0  2 - 2/x^2x^2 = 0  2 - 2 = 0
So YES, this is a solution.

(b)   y=x^2-1/x
y'=2x+1/x^2
y''=2-1/x^3
Plugging this information into the equation gives
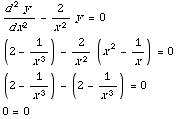
(d^2y)/dx^2 - 2/x^2y = 0  (2 - 1/x^3) - 2/x^2 (x^2 - 1/x) = 0  (2 - 1/x^3) - (2 - 1/x^3) = 0  0 = 0
So YES, this is a solution.

(c)   y=x^3
y'=3x^2
y''=6x
Plugging this information into the equation gives
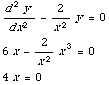
(d^2y)/dx^2 - 2/x^2y = 0  6x - 2/x^2x^3 = 0  4x = 0
NO, this is not a solution, because the function 4x does not equal the function 0.

(d)  y=0
Plugging this information into the equation gives
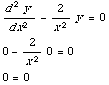
(d^2y)/dx^2 - 2/x^2y = 0  0 - 2/x^20 = 0  0 = 0
So YES, this is a solution