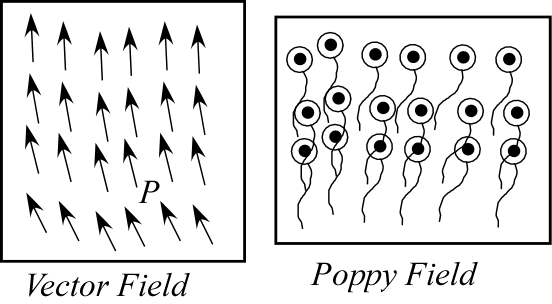
A vector field assigns a tangent vector v(P) to the tangent space TP at each point P of a manifold.
A vector field v acts on a function f to produce another function vf whose value at each point P is defined to be the directional derivative
vf |P =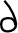 
C f(P)
= (C
f)'(P)
where C is one of the curves through the point P that belongs to the tangency class v(P).
