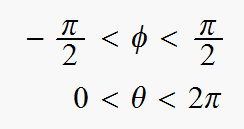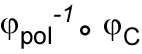 corresponds to the coordinate transformation equations:
corresponds to the coordinate transformation equations: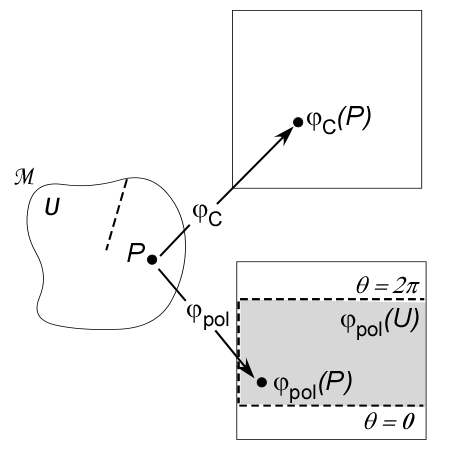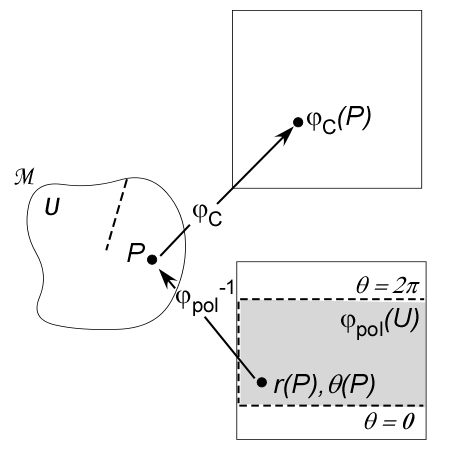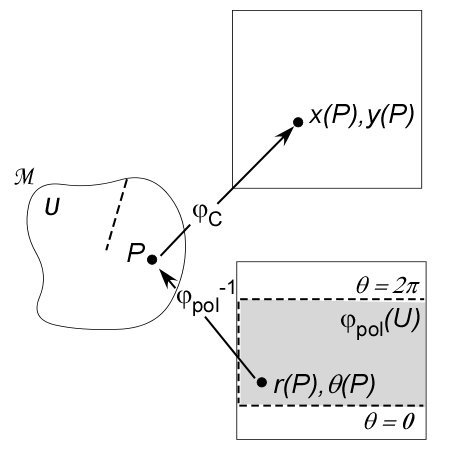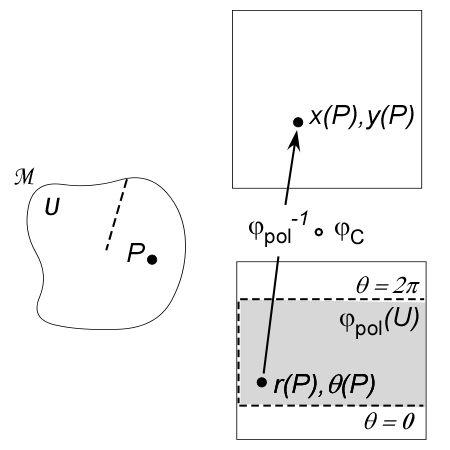
Reverse the other coordinate map, and the inverse coordinate transformation results.
The composite map 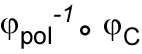 corresponds to the coordinate transformation equations:
corresponds to the coordinate transformation equations:
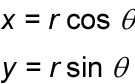
Suppose ![]() is a Cartesian coordinate map on a three dimensional space for which Euclidean geometry works. Choose a point
is a Cartesian coordinate map on a three dimensional space for which Euclidean geometry works. Choose a point ![]() and use Euclidean geometry to build a polar coordinate map
and use Euclidean geometry to build a polar coordinate map ![]() about that point.
about that point.
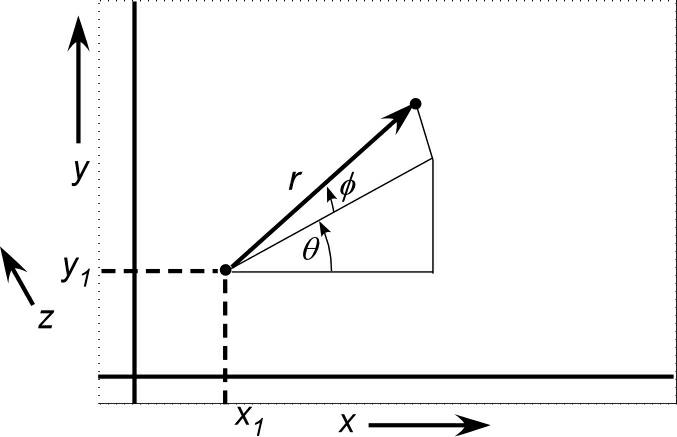
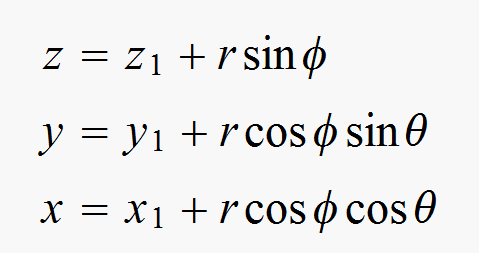
Another to way to say that is that they provide ![]() .
.
Still another way to say it is that they provide ![]()
The equations provide the coordinate transformation ![]() from polar coordinates to Cartesian coordinates.
from polar coordinates to Cartesian coordinates.
Now invert the equations to obtain the coordinate transformation ![]() from Cartesian coordinates to polar coordinates.
from Cartesian coordinates to polar coordinates.
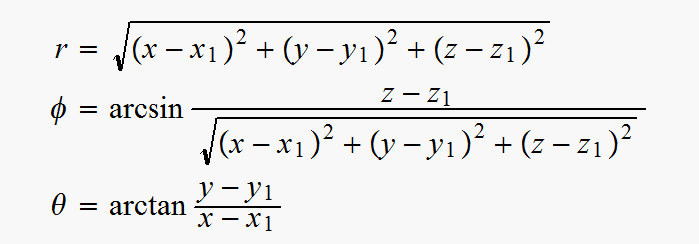
Notice that the inverse transformation fails for the Cartesian Coordinates x = x1, y = y1, z = z1, . The point labeled by that set of Cartesian coordinates does not have polar coordinates. Similarly, the inverse trigonometric functions are multiple valued unless the ranges of the angles are restricted: