Pearson’s r
The Pearson's correlation coefficient varies between -1 and +1 where:
r = 1 means the data is perfectly linear with a positive slope ( i.e., both variables tend to change in the same direction)
r = -1 means the data is perfectly linear with a negative slope ( i.e., both variables tend to change in different directions)
r = 0 means there is no linear association
r > 0 < 5 means there is a weak association
r > 5 < 8 means there is a moderate association
r > 8 means there is a strong association
The figure below shows some data sets and their correlation coefficients. The first data set has an r=0.996, the second has an r = -0.999 and the third has an r= -0.233
The formula for Pearson's r is:
Scatterplots! Scatterplots! Scatterplots!
Pearson's r is a numerical summary of the strength of the linear association between the variables. If the variables tend to go up and down together, the correlation coefficient will be positive. If the variables tend to go up and down in opposition with low values of one variable associated with high values of the other, the correlation coefficient will be negative.
"Tends
to" means the association holds "on average", not for any
arbitrary pair of observations, as the following scatterplot of weight against
height for a sample of older women shows. The correlation coefficient is
positive and height and weight tend to go up and down together. Yet, it is easy
to find pairs of people where the taller individual weighs less, as the points
in the two boxes illustrate.
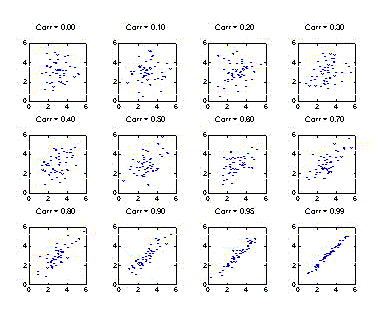How
do values of the correlation coefficient correspond to different data sets? As
the correlation coefficient increases in magnitude, the points become more
tightly concentrated about a straight line through the data. Two things should
be noted. First, correlations even as high as 0.6 don't look that different
from correlations of 0. I want to say that correlations of 0.6 and less don't
mean much if the goal is to predict individual values of one variable from the
other. The prediction error is nearly as great as we'd get by ignoring the
second variable and saying that everyone had a value of the first variable
equal to the overall mean! However, I'm afraid that this might be
misinterpreted as suggesting that all such associations are worthless. They
have important uses that we will discuss in detail when we consider linear
regression. Second, although the correlation can't exceed 1 in magnitude, there
is still a lot of variability left when the correlation is as high as 0.99.
Trouble!
The
pictures like those in the earlier displays are what one usually thinks of when
a correlation coefficient is presented. But the correlation coefficient is a
single number summary, a measure of linear association, and like all single
number summaries, it can give misleading results if not used with supplementary
information such as scatterplots. For example, data that are uniformly spread
throughout a circle will have a correlation coefficient of 0, but so, too, will
data that is symmetrically placed on the curve Y = X2! The reason
the correlation is zero is that high values of Y are associated with both high
and low values of X. Thus, here is an example of a correlation of zero even
where there is Y can be predicted perfectly from X!
To
further illustrate the problems of attempting to interpret a correlation
coefficient without looking at the corresponding scatterplot, consider this set
of scatterplots which duplicate most of the examples from pages 78-79 of Graphical
Methods for Data Analysis by Chambers, Cleveland, Kleiner, and Tukey. Each
data set has a correlation coefficient of 0.7.
1.
The correlation is 0 within the bulk of the data in the
lower left-hand corner. The outlier in the upper right hand corner increases
both means and makes the data lie predominantly in quadrants I and III. Check
with the source of the data to see if the outlier might be in error. Errors
like these often occur when a decimal point in both measurements is
accidentally shifted to the right. Even if there is no explanation for the
outlier, it should be set aside and the correlation coefficient or the
remaining data should be calculated. The report must include a statement of the
outlier's existence. It would be misleading to report the correlation based on
all of the data because it wouldn't represent the behavior of the bulk of the
data.
As discussed below, correlation coefficients are appropriate only when data are
obtained by drawing a random sample from a larger population. However,
sometimes correlation coefficients are mistakenly calculated when the values
one of the variables--X, say--are determined or constrained in advance by the
investigator. In such cases, the message or the outlier may be real, namely,
that over the full range of values, the two variables tend to increase and
decrease together. It's poor study design to have the answer determined by a
single observation and it places the analyst in an uncomfortable position. It
demands that we assume thr association is roughly linear over the entire range
and that the variability in Y will be no different for large X from what it is
for small X. Unfortunately, once the study has been conducted, there isn't much
that can be done about it. The outcome hinges on a single obsrevation.
2. Similar to 1. Check the outlier to see if it is in error. If not, report the correlation coefficient for all points except the outlier along with the warning that the outlier occurred. Unlike case 1 where the outlier is an outlier in both dimensions, here the outlier has a reasonable Y value and only a slightly unreasonable X value. It often happens that observations are two-dimensional outliers. They are unremarkable when each response is viewed individually in its histogram and do not show any aberrant behavior until they are viewed in two dimensions. Also, unlike case 1 where the outlier increases the magnitude of correlation coefficient, here the magnitude is decreased.
3. This sort of picture results when one variable is a component of the other, as in the case of (total energy intake, energy from fat). The correlation coefficient almost always has to be positive since increasing the total will tend to increase each component. In such cases, correlation coefficients are probably the wrong summaries to be using. The underlying research question should be reviewed
4. The two nearly straight lines in the display may be the result of plotting the combined data from two identifiable groups. In might be as simple as one line corresponding to men, the other to women. It would be misleading to report the single correlation coefficient without comment, even if no explanation manifests itself.
5. The correlation is zero within the two groups; the overall correlation of 0.7 is due to the differences between groups. Report that there are two groups and that the within group correlation is zero. In cases where the separation between the groups is greater, the comments from case 1 apply as well. It may be that the data are not a simple random sample from a larger population and the division between the two groups may be due to a conscious decision to exclude values in the middle of the range of X or Y. The correlation coefficient is an inappropriate summary of such data because its value is affected by the choice of X or Y values.
6. What most researchers think of when a correlation of 0.7 is reported.
7. A problem mentioned earlier. The correlation is not 1, yet the observations lie on a smooth curve. The correlation coefficient is 0.70 rather than 0 because here the curve is not symmetric. Higher values of Y tend to go with higher values of X. A correlation coefficient is an inappropriate numerical summary of this data. Either (i) derive an expression for the curve, (ii) transform the data so that the new variables have a linear relationship, or (iii) rethink the problem.
8. This is similar to case 5, but with a twist. Again, there are two groups, and the separation between them produces the positive overall correlation. But, here, the within-group correlation is negative! I would do my best to find out why there are two groups and report the within group correlations.
The moral of these displays is clear: ALWAYS LOOK AT THE SCATTERPLOTS!