Radiation Exposure – Shielding
  1. Concepts of shielding and the application of Half-Value Layers HVLs have been discussed in previous semester, however, there is a lot more to this so let us review old and learn new concepts

  2. Review
    1. The type of shielding required depends on the type of radiation
    2. Alpha particles require nothing more that a sheet of paper to be absorbed
    3. Beta particles require nothing more than a ¼ inch thick of plastic
    4. Gamma and x-rays require lead, concrete, or a lot of water
    5. Applications in nuclear medicine
      1. Alpha radiation is not used in nuclear medicine
      2. Some radiopharmaceuticals used in nuclear medicine have beta radiation associated with its decay
        1. Pure beta, such as 32 P would only require plastic for shielding
        2. A mixed emitter, such as 153Sm or 131I requires a combination of plastic and Pb to achieve adequate shielding. If lead is used without any plastic Bremsstrahlung radiation will occur, hence plastic is also required
  3. Gamma and X radiation
    1. Pending the energy of the photon lead will absorb the radiation through a series of pair production, Compton, and/or finally photoelectric
      1. If a gamma ray has an energy of 1.02 or greater MeV it will be absorbed by the nucleus of an atom, which could cause pair production (if the energy is less than 1.02 MeV go to the next step)
      2. 1019 keV or less and 511 keV gammas are produced by the annihilation undergo a series of Compton interactions
      3. Once the gamma ray’s energy is decreased enough it will finally be absorbed by photoelectric effect

    2. Shielding material – two points must be considered
      1. Thickness – the thicker the absorber the greater the shielding
      2. Density – the denser the absorber is the greater the shielding
      3. Hence the following formula shows the relationship between density (later referred to as ρ) of the material (gm/cm3) and thickness (later referred to as μ)  of the material (cm) of the same material. Consider this concept as density thickness, which is also referred to as  ρ/μ

        density-thicness.jpg - 6255 Bytes

      4. In addition
        1. The Z number does not always directly relate to density
        2. Density changes when the same element is in a solid, liquid, or gaseous state
        3. Can you think of a good example?

    3. Attenuation coefficient – is considered a unit for measuring the quantity of radiation being absorbed (there are two types)
    4. (1) Linear attenuation coefficient (μ)
      1. Is defined as the amount of or fraction of photons removed from a radiation field per cm of absorber(cm-1)
      2. The final answer is expressed as a constant % which is then multiplied by the amount of initial radiation being emitted
      3. Special comment - μ is the analog of the decay constant (λ)
        4. and we've get back to this in just a bit
      4. The ability for any material to absorb depends on
        1. Its thickness
        2. Its density (depends on it state)
        3. Energy gamma be absorbed
    5. (2) Mass attenuation coefficient (μ/ρ)
      1. Value is obtained by taken the linear attenuation coefficient and the density of the material
      2. Expressed as gm/cm2
    6. Relationship between linear and mass attenuation coefficient
      1. Linear attenuation (μ) varies depending on its state (gas, liquid, or water). The issue here is that the density will vary depending on its physical state. Therefore its density and thickness must be  considered when it is being used as an attenuator
        2. as is what needs to be considered when using μ to calculate attenuation
      2. Mass attenuation (μ/ρ) only relates to the density of the absorber (not its thickness) therefore the physical state of the absorber is not a factor
      3. Consider the following physical states of water and note the μ, ρ, and μ/ρ relationships

        4. 1 cm3 of water

        Water vapor

        Water liquid

        Water solid

        μ (cm-1)

        0.000128

        0.214

        0.196

        ρ (gm/cm3)

        1.00598

        1.0

        0.917

        μ/ρ (cm2/gm)

        0.214

        0.214

        0.214

      4. Shielding formulas uses linear attenuation coefficient
    7. Attenuation in the photoelectric range
      1. In general one would think that as the energy of gamma radiation increases the interaction with the absorber would have an exponential curve, however, while the curve general looks exponential there are to deviations that occur within it
      2. If the gamma energy is close to the binding energy of the L or K shell electron of the attenuator, photoelectric effect is less likely to occur and more attenuation will be needed. This is because photon interacts with electron’s binding energy
        1. The L shell interaction occurs at 20 keV and is referred to as the L-edge
        2. The K shell interaction occurs at 88 keV and is referred to as the K-edge
        3. Application to Nuclear Medicine? 133Xe requires more shielding that 99mTc because the 81 keV gamma is effected by the K-edge
    8. Attenuation in the Compton range
      1. Consider the relationship – electrons per gram, similar to density, however, electrons replace cm
      2. The greater the number of electrons per gram the greater the probability that a gamma ray will interact in an absorber via Compton
      3. Just because an absorber is high in density does not necessary mean that it has a greater number of electrons
        1. Ag has a density of 10.5 with 2.751 x 1024 electrons
        2. Pb has a density of 11.35 with 2.701 x 1024 electrons
        3. Therefore Ag is a better attenuator that Pb
        4. Why doesn’t nuclear medicine use Ag instead of Pb for shielding?
        5. Interesting point – depleted uranium has greater density and electrons when compared to the above: density = 18.68 and electrons = 4.352 x 1024. When high levels of radiation require shielding, depleted uranium is considered
  4. Shielding Formula

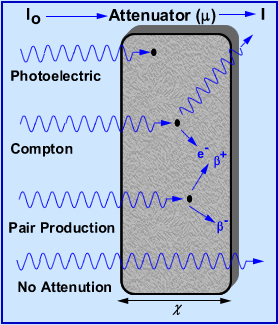
    5. LET diagram

    1. The above diagram gives a graphical display on the process in which gamma rays are of attenuated
      1. Note the relationship between the diagram and the attenuation formula specifically with: I, lo, :, and P
      2. The behavior of photoelectric, Compton, and pair production can be seen
      3. Remember, the only way a gamma ray can be attenuated is when it actually reacts with an electron or the nucleus of the atom

      attenuationform.jpg - 1881 Bytes
    2. From the above formula
      1. I = radiation intensity after shielding
      2. Io = radiation intensity before shielding
      3. E = natural log of 2
      4. μ = linear attenuation coefficient in cm-1
      5. χ = thickness of the shield in cm

    3. If the original gamma intensity is 211 mr/hr for 99mTc, the attenuator (Pb) is 2.5 mm in length, and attenuation coefficient is 23 what is the new gamma intensity? This calculation is similar to the decay formula

      Let's take a look at the different ways you can use the attenuation formula

      1. While this is an approach used to determining the attenuation of gamma radiation after shielding, in nuclear medicine we can also apply the concept of half-value layer (HVL).  This concept ties into the shielding formula noted above, however, it is "more basic" in its approach.
      2. To have an attenuator that has a value of 1 HVL means that it reduces the intensity of radiation by 1/2.  Similar to the value x in the formula above where the density of the shield determines the HVL.  HVL is also determined by the amount of energy being emitted by the incoming gamma.  In addition, the greater the Eγ the need more shielding and/or greater density is required Below are some HVL values

        3. HVL - Attenuator in gm/cm3 Pb - 11.34 H2O - 1.0 NaI - 3.67
        140 keV 0.0256 cm 4.53 cm 0.278 cm
        364 keV 0.219 cm 6.245 cm 1.51 cm
        511 keV 0.4021 cm 7.22 cm 2.12 cm

      3. Therefore, to reduce an incoming gamma by 50% with an Eγ of 140 keV you would need 0.256 mm of lead.  How much NaI would you need to reduce a positron gamma to 12.5%?


      4. Let's first look at HVLs (the easy way).  The original rate of exposure for 99mTc is 734.5 mr/hr.  If 1.24 mm of Pb is used as a shielding device.  What is the new rate of exposure?


      5. Using the attenuation formula one can still apply HVL, however, the process becomes somewhat more complicated.  Note the comparison below.  We are solving for the new radiation exposure after shielding.  The following is given:  Io - 75.2 mr/hr, HVL value - 0.4021, and the thickness of the attenuator - 2.1 cm.  The results are noted below:  attenuation formula to the right and HVL formula to the left.


      6. Let's now change our approach just a little.  This time let the unknown be HVL thickness, given the following:  Initial intensity is 422 mr/hr and after shielding the exposure rate is 156 mr/hr.  The thickness of the shield is 6.0 cm.  Solved below.  (Note:  you really don't need to know the energy of the incoming gamma.

      Tying it all together you can look at the different formulas for decay and attenuation are realize that there is a direct relationship with the center point being the natural log of 2.  See PDF file.

      Return to the beginning of the document
      Return to the Table of Contents